flowchart LR
A0["A"]
I0["Ω"]
I0 --X--> A0
A1(["a"])
I1(["●
●
●"])
I1 --> A1
A2(["b"])
I2(["●
●"])
I2 --> A2
A3(["c"])
I3(["●
●
●
●"])
I3 --> A3
3 Probabilités
\[ \newcommand{\croD}{[} \newcommand{\croG}{]} \newcommand{\Nat}{\mathbb{N}} \newcommand{\Reel}{\mathbb{R}} \newcommand{\Univ}{\Omega} \newcommand{\boolD}{\mathbf{2}} \newcommand{\vrai}{\mathtt{V}} \newcommand{\faux}{\mathtt{F}} \newcommand{\fctn}[3]{#1\ :\ #2 \rightarrow #3} \newcommand{\idF}{\mathtt{id}} \newcommand{\card}[1]{\mathtt{card}\ #1} \newcommand{\arrangement}[2]{\mathtt{A}_{#1}^{#2}} \newcommand{\combi}[2]{\mathtt{C}_{#1}^{#2}} \newcommand{\esper}{\mathbb{E}} \newcommand{\variance}{\mathbb{V}} \newcommand{\covariance}{\mathtt{co}\mathbb{V}} \newcommand{\corr}{\mathtt{Cor}} \newcommand{\reduc}{\nu} \newcommand{\ecartT}{\mathbf{\sigma}} \newcommand{\esperI}{\mathtt{E}} \newcommand{\moment}{\mathbb{M}} \newcommand{\proba}{\mathbb{P}} \newcommand{\probaCond}[2]{\mathbb{P}\ (#1 \mid #2)} \newcommand{\depl}[2]{\mathcal{CH}\ {#1}\ {#2}} \newcommand{\coefBi}[2]{\left(^{#1}_{#2}\right)} \newcommand{\blanc}{\mathtt{B}} \newcommand{\noir}{\mathtt{N}} \newcommand{\pFine}{\preceq} \newcommand{\iterOp}[3]{{#1}^{{}_{#2}{#3}}} \newcommand{\centrage}{\pi_\mathtt{C}} \newcommand{\partition}[2]{\{{#1}\}_{#2}} \newcommand{\seqVide}{\varepsilon} \]
AFFAIRE(plan général pour les probabilités discrètes (univers fini ou dénombrable, N-0 univers fini uniquement, cas dénombrable traitable ? niveau N+3 ? pas de trace au programmes sup et spé semble-t-il) - Kolmogorov : une théorie élémentaire pour des univers finis, puis le passage à l’infini, dénombrable ou non : certainement la meilleure solution.
- introduction, vue catégorique :
- objets : espaces probabilisés (univers d’issues muni d’une fonction de probabilité)
- flèches : variables aléatoires (fonction classique transportant la probabilité) telles que la probabilité induite est celle de la cible
- espace probabilisé - objets de la catégorie
- fonction de probabilité
- notion d’évènement : d’ensemble à prédicat
- propriétés de la fonction de probabilité - préparation à l’axiomatisation
- variable aléatoire - flèches de la catégorie
- décomposition canonique, partition, système complet d’évènement, loi induite
- indicateurs statistiques : espérance, variance
- interprétation géométrique : covariance comme produit scalaire
- trait distinctif de la théorie : l’indépendance
- modèle universel pour l’interprétation : indépendace des expériences et conséquences
- définition de l’indépendance inspirée du modèle : / système complet, / variables aléatoires
- interprétation dans le modèle
- probabilité conditionnelle (théorie de Bayes, cf. cours De Kolmogorov)
- lois marginales
- théorie de l’indépendance mutuelle
- stabilité par restriction
- réciproque fausse : démonstration via les degrés de liberté
- stabilité par intersection
- stabilité par regroupement
- relation avec la corrélation
- stabilité par restriction
)
3.1 Transporter l’aléatoire : les variables aléatoires
Soit \(\Univ{}\) l’ensemble fini des issues1, appelé l’univers. L’aléatoire est défini sur l’univers par une fonction de probabilité \(\fctn{\proba{}}{\Univ{}}{\croD{}0,1\croG{}}\) qui répartit la valeur unité (représentant la certitude) entre toutes les issues :
\[ \sum_{i \in \Univ{}} \proba{}\ i = 1. \]
La fonction de probabilité correspond donc à une répartition de la probabilité. Elle s’étend naturellement à toute partie \(E\) de l’univers, appelée évènement : \[ \proba{}\ E := \sum_{i \in E} \proba{}\ i. \] Or les parties de \(\Univ{}\) sont en correspondance bi-univoques avec les prédicats sur \(\Univ{}\) (AFFAIRE(lien vers cours - équivalence fondamentale ensemble-prédicat\(i \in E \leftrightarrow E\ i\)). Par la suite nous utilisons cette équivalence, parfois tacitement, pour passer de l’une à l’autre des représentations, des évènements aux prédicats ou l’inverse ; par exemple, nous pouvons interpréter l’extension de la fonction de probabilité aux évènements comme une extension à tout prédicat $E $ via l’équivalence fondamentale : \[ \proba{}\ E := \sum_{i \in \Univ{} \mid E\ i} \proba{}\ i. \]
L’univers muni de sa fonction de probabilité devient un espace probabilisé. Toute fonction \(\fctn{X}{\Univ{}}{A}\) partant de l’espace probabilisé \(\Univ{}\) est appelée une variable aléatoire. C’est une qualification de la fonction, qui effectivement varie aléatoirement. S’il n’y avait aucun aléa, la fonction de probabilité \(\proba{}\) serait concentrée en une valeur : elle serait partout nulle sauf en une issue où elle vaudrait un. Autrement dit, elle correspondrait à un choix déterministe d’une unique issue. La composition de ce choix avec la fonction \(X\) donnerait alors une unique valeur de \(A\), bref une constante. Avec la répartition de l’unité entre les issues, la composition devient variable, aléatoirement. Pour pouvoir composer des variables aléatoires, on considère des ensembles d’arrivée finis. Il arrive parfois ci-dessous d’utiliser un ensemble d’arrivée infini, comme \(\Reel{}\), pour exprimer la nature des valeurs produites : la restriction à l’image de \(X\), un ensemble fini puisque l’univers l’est, est alors implicite.
Une variable aléatoire \(\fctn{X}{\Univ{}}{A}\) a pour effet de transporter la structure aléatoire de l’univers \(\Univ{}\) à l’ensemble d’arrivée \(A.\) La fonction de probabilité induite par la variable aléatoire, notée \(\proba{}_X\) associe à tout élément \(a\) de \(A\) la probabilité de l’évènement formé de tous les antécédents de \(a\). \[ \proba{}_X\ a := \proba{} (\{i \in \Univ{} \mid X\ i = a\}). \]
Plutôt que d’utiliser une notation ensembliste, on préfère recourir au prédicat équivalent \(X = a,\) soit la fonction \((i \mapsto X\ i = a)\) et écrire, avec l’avantage de la simplicité :
\[ \proba{}_X\ a := \proba{}\ (X = a). \]
La fonction induite de probabilité est appelée la loi de probabilité de la variable aléatoire \(X\). Par définition de la probabilité d’un évènement comme la somme de la probabilité des issues qu’il contient, on obtient la caractérisation suivante de la loi de probabilité.
\[ \proba{}\ (X = a) = \sum_{i \in \Univ{} \mid X\ i = a} (\proba{}\ i). \]
Elle résulte directement de la décomposition canonique de \(X\), qui induit une partition des issues suivant leur image par \(X\).
AFFAIRE(lien vers cours - décomposition canonique, partition, congruence)
Rappelons qu’une partition de l’univers \(\Univ{}\) est un ensemble de parties non vides et disjointes deux à deux, qui recouvrent par union l’univers \(\Univ{}.\) Comme chaque partie de l’univers est un évènement, une partition dans le cadre probabiliste est appelée un système complet d’évènements. Le système complet induit par la variable aléatoire \(X\) est l’ensemble \(\partition{X = c}{c\in X\ \Univ{}}.\) On dit que deux variables aléatoires \(\fctn{X}{\Univ{}}{A}\) et \(\fctn{Y}{\Univ{}}{B}\) sont congruentes si elles induisent le même système complet d’évènements. C’est une relation d’équivalence qui oublie la valeur prise par la variable aléatoire mais retient la manière dont la probabilité est induite : en effet, chaque classe d’équivalence est en correspondance bi-univoque avec un système complet dont les évènements donnent les probabilités induites.
À côté de cette première équivalence induite par la partition de l’univers des issues, d’autres peuvent être définies, qui impliquent la loi de probabilité induite sur l’ensemble d’arrivée. On peut définir une équivalence en loi entre les variables aléatoires \(\fctn{X_1}{\Univ{}}{A_1}\) et \(\fctn{X_2}{\Univ{}}{A_2}\) : \[ \forall a \in A_1 \cup A_2, \proba{}\ (X_1 = a) = \proba{}\ (X_2 = a), \] ce qui implique qu’en dehors de l’intersection de \(A_1\) et de \(A_2\), les probabilités induites sont nulles. Bien sûr, les variables aléatoires équivalentes en loi peuvent différer suivant la manière dont elles associent aux issues une valeur dans l’ensemble d’arrivée, et ainsi ne pas être congruentes. Par exemple, pour un lancer de dé, la variable qui affirme que la valeur est supérieure à cinq et celle qui affirme que la valeur est inférieure à deux ont la même loi induite sur l’algèbre de Boole2 mais ne sont pas congruentes, puisqu’associées aux partitions \(\{\{5, 6\}, \{1, 2, 3, 4\}\}\) et \(\{\{1, 2\}, \{3, 4, 5, 6\}\}\) respectivement. On peut aussi définir une autre équivalence intermédiaire entre l’égalité et l’équivalence en loi : c’est l’égalité presque sûre. Deux variables aléatoires \(\fctn{X_1}{\Univ{}}{A_1}\) et \(\fctn{X_2}{\Univ{}}{A_2}\) sont presque sûrement égales si l’évènement formé des issues où elles diffèrent est négligeable3 : \[ \proba{}\ (X_1 \neq X_2) = 0, \] ou alternativement si l’évènement formé des issues où elles sont égales est presque sûr4 : \[ \proba{}\ (X_1 = X_2) = 1. \] Cette égalité presque sûre implique l’équivalence en loi puisque pour tout \(a \in A_1 \cup A_2\), \[ \begin{array}{rcl} \proba{}\ (X_1 = a) &=& \proba{}\ (X_1 = a) \wedge (X_2 = a) + \proba{}\ (X_1 = a) \wedge (X_2 \neq a) \\ &=& \proba{}\ (X_1 = a) \wedge (X_2 = a) \\ &=&\proba{}\ (X_1 = a) \wedge (X_2 = a) + \proba{}\ (X_1 \neq a) \wedge (X_2 = a) \\ &=& \proba{}\ (X_2 = a).\\ \end{array} \]
Prolongeant la notion d’égalité presque sûre entre variables aléatoires, la comparaison presque sûre de deux variables aléatoires \(X_1\) et \(X_2\) se définit par la certitude du résultat : on dit que \(X_1\) est strictement inférieur à \(X_2\) presque sûrement si \(\proba{}\ (X_1 < X_2) = 1\).
Récapitulons : les variables aléatoires sont intéressantes parce qu’elles permettent de transporter une structure aléatoire d’un ensemble à un autre. Par exemple, si à chaque issue, on associe un gain, il est naturel d’évaluer la probabilité de chaque gain possible. Plusieurs relations d’équivalence ou d’ordre permettent de comparer deux variables aléatoires. Cependant si le gain est numérique, il devient possible de mesurer la proximité des variables en réalisant des calculs comme celui de la moyenne possible des gains, l’espérance de gain, ou celui de la dispersion relativement à la moyenne. C’est la question que nous étudions désormais.
Au préalable, comme les variables aléatoires sont des fonctions, elles héritent de la structure algébrique dee ensembles d’arrivée. En effet toute opération binaire \(\fctn{\star}{A_1\times A_2}{A_3}\) s’étend aux fonctions sur \(\Univ{}\) de manière naturelle, point par point : étant donné deux fonctions \(\fctn{X_1}{\Univ{}}{A_1}\) et \(\fctn{X_2}{\Univ{}}{A_2}\), la fonction \(\fctn{X_1 \star X_2}{\Univ{}}{A_3}\) est définie par \((X_1\star X_2)\ x := (X_1\ x) \star (X_2\ x)\). Cette extension est également possible pour des opérations unaires, comme l’opposition \((x \mapsto -x)\) ou l’inversion \((x \mapsto 1/x)\) (pour les fonctions ne s’annulant jamais), ou des opérations externes comme la multiplication par un scalaire \((\lambda, x \mapsto \lambda * x)\).
Par exemple, on peut penser à la construction de couples : on note \(\fctn{(X_1, X_2)}{\Univ{}}{A_3}\) la fonction qui à \(x\) associe \((X_1\ x, X_2\ x).\) Si les variables aléatoires sont à valeurs réelles, étant donné deux variables aléatoires \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}},\) il est possible de construire les variables aléatoires \(X + Y\) et \(X * Y\), \(\lambda * X\) pour tout scalaire réel \(\lambda,\) et \(X^k\) pour tout entier \(k\), naturel ou relatif si \(X\) ne s’annule jamais.
3.1.1 Indicateurs statistiques : des moments d’une variable aléatoire à l’espérance et la variance
Nous nous intéressons désormais à des variables aléatoires numériques, soit à des fonctions à valeurs réelles. Développons des indicateurs statistiques, en considérant les probabilités comme des pondérations.
Définition 3.1 (Moments d’une variable aléatoire numérique) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Pour tout entier naturel \(k\), le moment d’ordre \(k\) de \(X\) est la somme pondérée par les probabilités induites des puissances \(k\)-ièmes des valeurs de \(X :\) \[ \moment{}_k\ X := \sum_{v \in (X\ \Univ{})} v^k * (\proba{}\ (X = v)). \]
Les moments ne dépendent que de la loi de probabilité de la variable aléatoire.
Proposition 3.1 (Égalité des moments de deux variables aléatoires équivalentes en loi) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) deux variables aléatoires équivalentes en loi. Alors pour tout entier naturel \(k,\) le moment d’ordre \(k\) de \(X\) est égal au moment d’ordre \(k\) de \(Y :\) \[ \moment{}_k\ X = \moment{}_k\ Y. \]
Bien sûr, cette proposition implique que si deux variables aléatoires sont presque sûrement égales, alors elles ont les même moments.
Plutôt que de calculer le moment à partir de la loi de probabilité et de l’image de l’univers \(\Univ{}\) par \(X\), nous pouvons le calculer directement à partir des issues, en utilisant la décomposition canonique de \(X.\)
Proposition 3.2 (Calcul des moments d’une variable aléatoire numérique à partir des issues) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Pour tout entier naturel \(k\), le moment d’ordre \(k\) de \(X\) est égal à la somme pondérée par les probabilités des puissances \(X^k\) appliquées aux issues : \[ \moment{}_{k}\ X = \sum_{i \in \Univ{}} (X\ i)^k * (\proba{}\ i). \]
Il existe donc deux manières de calculer un moment, en sommant
- les valeurs aléatoires prises par la puissance de la variable aléatoire pondérées par leur probabilité induite, ou
- les images des issues par la puissance de la variable aléatoire pondérées par leur probabilité originale.
Souvent l’une des deux manières mène à des calculs simplifiés : le calcul sur l’ensemble d’arrivée peut bénéficier de l’agrégation des issues dans la probabilité induite alors que le calcul sur les issues peut bénéficier des propriétés algébriques des variables aléatoires. En voici une illustration, lors du calcul d’un moment à un ordre égal à un produit.
Corollaire 3.1 (Moment à un ordre produit) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Pour tous entiers naturels \(k\) et \(l\), le moment d’ordre \(k * l\) de \(X\) est égal au moment d’ordre \(l\) de la puissance \(X^k :\) \[ \moment{}_{k *l}\ X = \moment{}_{l}\ X^k. \]
On déduit aussi de cette caractérisation la croissance des moments.
Corollaire 3.2 (Croissance des moments) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{X}{\Univ{}}{\Reel{}}\) deux variables aléatoires.
- Supposons que \(X\) soit inférieure à \(Y\) presque sûrement : \[ \proba{}\ (X \leq Y) = 1. \] Alors pour tout entier naturel impair \(k\), le moment d’ordre \(k\) de \(X\) est inférieur ou égal à celui de \(Y\) : \[ \moment{}_{k}\ X \leq \moment{}_{k}\ Y. \]
- Supposons que \(X^2\) soit inférieure à \(Y^2\) presque sûrement : \[ \proba{}\ (X^2 \leq Y^2) = 1. \] Alors pour tout entier naturel pair \(k\), le moment d’ordre \(k\) de \(X\) est inférieur ou égal à celui de \(Y\) : \[ \moment{}_{k}\ X \leq \moment{}_{k}\ Y. \]
À partir des moments, plusieurs indicateurs peuvent être définis, dont deux fondamentaux : l’espérance exprimant la moyenne pondérée par les probabilités induites des valeurs prises par la variable aléatoire, et la variance exprimant la dispersion relativement à la moyenne, mesurée par la moyenne pondérée par les probabilités induites des carrés des distances entre les valeurs prises par la variable aléatoire et la moyenne, ou l’écart-type pour normaliser, soit la racine carrée de la variance.
Définition 3.2 (Espérance, variance et écart-type) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire.
- Espérance de \(X :\) \(\esper{}\ X := \moment{}_1\ X\).
- Variance de \(X :\) \(\variance{}\ X := \moment{}_2\ (X - (\esper{}\ X))\).
- Écart-type de \(X :\) \(\ecartT{}\ X := \sqrt{\variance{}\ X}\).
Par exemple, si la fonction \(X\) est constante, toujours égale au réel \(k\), alors l’espérance est \(k\) et la variance comme l’écart-type sont nuls, faute de dispersion.
Une fois que l’espérance est définie, il est possible de se passer de la notion de moment, grâce à ce lemme de transfert, qui permet de calculer l’espérance non seulement sur l’ensemble image mais aussi sur tout ensemble intermédiaire, comme l’illustre la Figure 3.2.
flowchart LR
A0["A"]
I0["Ω"]
I0 --X--> A0
B0["B"]
A0 --f--> B0
B1(["b"])
A1(["a1"])
A1 --> B1
A1(["a1"])
I1(["●
●
●"])
I1 --> A1
A2(["a2"])
A2 --> B1
I2(["●
●"])
I2 --> A2
A3(["a3"])
A3 --> B1
I3(["●
●
●
●"])
I3 --> A3
Lemme 3.1 (Transfert du calcul de l’espérance) Soient \(\fctn{X}{\Univ{}}{A}\) une variable aléatoire et \(\fctn{f}{A}{\Reel{}}\) une fonction d’évaluation. Alors l’’espérance de la variable aléatoire \(f \circ X\) est égale à la moyenne pondérée par les probabilités induites par \(X\) des images par \(f :\) \[ \esper{}\ f \circ X = \sum_{v \in (X\ \Univ{})} (f\ v) * (\proba{}\ (X = v)). \]
Appliquons ce lemme de transfert à la fonction puissance.
Corollaire 3.3 (Moment comme espérance d’une puissance) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire et \(k\) un entier naturel. Alors \[ \moment{}_k\ X = \esper{}\ X^k. \]
En particulier, la variance peut se calculer à partir de l’espérance. La démonstration utilise la linéarité de l’espérance, présentée juste après (voir la Proposition 3.4).
Proposition 3.3 (Variance comme espérance d’un carré - Théorème de König-Huygens) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Alors \[ \variance{}\ X = (\esper{}\ X^2) - (\esper{}\ X)^2. \]
Cette formule amène à la pratique suivante, plutôt économe, pour calculer la variance : calculer l’espérance de \(X\), puis l’espérance de \(X^2\), en déduire la variance par la formule de König-Huygens.
3.1.2 Approche géométrique : les variables aléatoires comme vecteurs
La Proposition 3.2 permet de déduire des propriétés algébriques pour l’espérance et la variance ou l’écart-type en calculant à partir des issues.
Proposition 3.4 (Linéarité de l’espérance) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) deux variables aléatoires. Alors pour tous scalaires réels \(\alpha\) et \(\beta\), on a \[ \esper{}\ (\alpha * X + \beta * Y) = \alpha * (\esper{}\ X) + \beta * (\esper{}\ Y). \]
La Proposition 3.2 montre aussi que pour des moments d’ordre strictement supérieur à \(1\), comme la variance, il ne peut y avoir de linéarité, sans hypothèses supplémentaires, à cause des puissances à développer. De manière générale, pour bien comprendre les propriétés algébriques, il est utile d’élaborer la structure de l’ensemble des variables aléatoires numériques définies sur l’univers \(\Univ{}\). Muni de l’addition et de la multiplication par un scalaire, il devient un espace vectoriel : une variable aléatoire peut être vue comme un vecteur, dont les coordonnées sont indexées par les issues. Cet espace vectoriel peut être muni d’un produit scalaire, une variante de celui classique : plutôt que de considérer la somme des produits des coordonnées, on utilise la moyenne pondérée par les probabilités. S’il existe une issue de probabilité nulle, alors cette moyenne pondérée n’est pas exactement un produit scalaire : les propriétés sont seulement vérifiées presque sûrement. Malgré cette réserve, nous utilisons la terminologie géométrique.
Définition 3.3 (Produit scalaire de variables aléatoires numériques) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) deux variables aléatoires numériques. Le produit scalaire de \(X\) et de \(Y\) est défini par l’espérance de leurs produits \(X * Y,\) soit \[ \esper{}\ (X * Y). \]
La norme de la variable aléatoire \(X\) est définie ainsi : \[ \| X \| := \sqrt{\esper{}\ X^2}. \]
Le produit scalaire peut être calculé d’une manière naturelle en itérant sur les issues : \[ \esper{}\ (X * Y) = \sum_{i \in \Univ{}} (X\ i) * (Y\ i) * (\proba{}\ i). \] Mais il peut être aussi calculé en itérant sur les valeurs prises par le produit \(X*Y\), \[ \esper{}\ (X * Y) = \sum_{v \in (X * Y)\ \Univ{}} v * (\proba{}\ (X * Y = v)). \] ce qui n’est pas pratique à cause du produit. Il est préférable de transférer le calcul à l’étape précédente, en itérant sur les couples appartenant à \((X\ \Univ{})\times (Y\ \Univ{})\) avant de réaliser le produit. Appliquons le Lemme 3.1 : \[ \esper{}\ (X * Y) = \sum_{(x, y) \in (X\ \Univ{})\times (Y\ \Univ{})} x * y * (\proba{}\ (X = x)\wedge(Y = y)). \]
Développons la théorie en nous inspirant de la géométrie euclidienne.
Proposition 3.5 (Propriétés du produit scalaire de variables aléatoires numériques) Soient \(\fctn{X}{\Univ{}}{\Reel{}}, \fctn{Y}{\Univ{}}{\Reel{}}\) et \(\fctn{Z}{\Univ{}}{\Reel{}}\) des variables aléatoires numériques. Le produit scalaire de variables aléatoires vérifie les propriétés suivantes.
- Symétrie5 – \(\esper{}\ (X * Y) = \esper{}\ (Y * X).\)
- Bilinéarité – \(\forall (\alpha, \beta \in \Reel{}), \esper{}\ ((\alpha * X + \beta * Y) * Z) = \alpha * (\esper{}\ (X * Z)) + \beta * (\esper{}\ (Y * Z)).\)
- Positivité stricte - \(\esper{} (X * X) \geq 0\), avec \((\esper{} (X * X) = 0) \leftrightarrow (\proba{}\ (X = 0) = 1.\)
Il est possible de déduire de ces propriétés génériques définissant un produit scalaire deux inégalités équivalentes. Noter que l’inégalité de Cauchy-Schwartz justifie l’expression du produit scalaire à l’aide des normes et du cosinus.
Proposition 3.6 (Inégalité triangulaire - Inégalité de Cauchy-Schwarz) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) des variables aléatoires numériques. Alors les inégalités suivantes sont vérifiées.
- Inégalité de Cauchy-Schwarz – \(|\esper{}\ (X * Y)| \leq \|X\| * \|Y\|.\)
- Inégalité triangulaire6 – \(\| X + Y \| \leq \|X\| + \| Y \|.\)
On dit qu’une variable aléatoire est centrée si son espérance est nulle. Du fait de la linéarité de l’espérance, c’est un sous-espace vectoriel de l’ensemble des variables aléatoires, défini comme le noyau de l’espérance. Toute variable aléatoire \(X\) se décompose en une variable aléatoire centrée \(X - (\esper{}\ X)\) et une variable aléatoire constante \(\esper{}\ X.\) Les deux sous-espaces vectoriels formés des variables aléatoires centrées et des variables aléatoires constantes respectivement sont orthogonaux : si \(X\) est d’espérance nulle et \(Y\) est constant, alors \[
\esper{}\ (X * Y) = Y * \esper{}\ X = 0.
\] La projection \(\centrage{} := \idF{} - \esper{}\) est appelée la fonction de centrage. Elle est souvent utilisée pour étudier la dispersion : rappelons que la variance de \(X\), \(\variance{}\ X,\) est le carré de la norme \(\| \centrage{}\ X \|^2,\) son écart-type \(\ecartT{}\ X\) étant la norme \(\| \centrage{}\ X \|.\) Pour deux variables \(X\) et \(Y,\) la covariance de \(X\) et de \(Y\) est le produit scalaire des variables aléatoires centrées associées \[
\covariance{}\ X \ Y := \esper{}\ ((\centrage{}\ X) * (\centrage{}\ Y)).
\] Le cosinus de l’angle entre \(\centrage{}\ X\) et \(\centrage{}\ Y\) est appelé le coefficient de corrélation linéaire :
\[
\corr{}\ X\ Y := \frac{\covariance{}\ X\ Y}{(\ecartT{}\ X)*(\ecartT{}\ Y)}.
\] En plus du centrage, la normalisation est utile pour rapporter à une même échelle. À une variable aléatoire \(X,\) on associe la variable centrée et unitaire8 \[
(\centrage{}\ X)/\| \centrage{}\ X \|,
\] soit \[
(X - (\esper{}\ X))/(\ecartT{}\ X).
\] Une telle variable est dite réduite : son espérance est nulle et sa variance vaut un. On la note \(\reduc{}\ X.\) Le produit scalaire des deux variables réduites \(\reduc{}\ X\) et \(\reduc{}\ Y\), soit \(\esper{} ((\reduc{}\ X)*(\reduc{}\ Y))\) est alors le coefficient de corrélation \(\corr{}\ X\ Y\).
Le centrage est utile parce qu’il permet de passer d’une relation affine à une relation linéaire, une simplification pertinente dans de nombreux contextes (AFFAIRE lien vers suites récurrentes affines + équa diff). Supposons une relation affine entre \(X\) et \(Y :\) \[ Y = \alpha * X + \beta. \] Par linéarité de l’espérance, on a \(\esper{}\ Y = \alpha * (\esper{}\ X) + \beta,\) puis par soustraction \[ Y - (\esper{}\ Y) = \alpha * (X - (\esper{}\ X)), \] soit \(\centrage{}\ Y = \alpha * (\centrage{}\ X).\) On peut alors calculer \(|\alpha|\) comme le rapport \(\|\centrage{}\ Y\|/\|\centrage{}\ X\|\), ce qui donne \[ \reduc{}\ Y = \lambda * (\reduc{}\ X), \] avec \(|\lambda| = 1.\) L’équation entre formes réduites est non seulement linéaire mais normalisée, avec un coefficient de valeur absolue unitaire.
Étudions donc la relation entre deux variables aléatoires réduites \(\reduc{}\ X\) et \(\reduc{}\ Y.\) Nous nous intéressons aux relations linéaires et à la question de la régression9 : pour quelle valeur du scalaire \(\lambda\) la variable \(\lambda * (\reduc{}\ X)\) se rapproche-t-elle le plus de la variable \(\reduc{}\ Y\) ? Pour distance entre les variables aléatoires, prenons la norme \(\|(\reduc{}\ Y) - \lambda * (\reduc{}\ X)\|\) et évaluons son carré. \[ \begin{array}{rcl} \| (\reduc{}\ Y) - \lambda * (\reduc{}\ X)\|^2 & = & \esper{}\ ((\reduc{}\ Y) - \lambda * (\reduc{}\ X))^2 \\ & = & 1 - 2 * (\corr{}\ X\ Y) * \lambda + \lambda^2 \\ & = & (\lambda - (\corr{}\ X\ Y))^2 + 1 - (\corr{}\ X\ Y)^2.\\ \end{array} \] La distance est donc minimale en \(\lambda = \corr{}\ X\ Y\), où elle vaut alors \(\sqrt{1 - (\corr{}\ X\ Y)^2}.\) Si le coefficient de corrélation vaut \(1,\) alors \(\reduc{}\ X\) et \(\reduc{}\ Y\) sont presque sûrement égaux, et réciproquement d’ailleurs : la corrélation est maximale et la variable \(Y\) peut être réduite à \(X\) par une relation affine. De même si le coefficient de corrélation vaut \(-1\), \(Y\) peut être réduite à \(X\) par une relation affine. Géométriquement, les vecteurs \(\reduc{}\ X\) et \(\reduc{}\ Y\) sont colinéaires. Si le coefficient de corrélation vaut \(0,\) alors la meilleure réduction de \(Y\) à \(X\) par une relation affine \(Y = \alpha * X + \beta\) 0s’obtient avec un coefficient directeur \(\alpha\) nul, autrement dit sans \(X,\) et pour toute valeur non nulle de \(\lambda,\) la distance entre \(\reduc{}\ Y\) et \(\lambda*(\reduc{}\ X)\) est strictement supérieure à \(1.\) Bref, il est impossible de réduire \(Y\) à \(X :\) on dit que \(X\) et \(Y\) sont décorrélés. Géométriquement, la décorrélation correspond à l’orthogonalité.
On peut représenter la relation entre les variables \(X\) et \(Y\) par un nuage de points dans un espace à deux dimensions. Chaque point du nuage a pour coordonnée \((X\ i, Y i)\) et pour pondération \(\proba{}\ i,\) où \(i\) parcourt l’univers \(\Univ{}.\)
Voici quelques exemples définis sur un petit univers : les lettres \(A, B, \ldots\) correspondent aux issues et sont pondérées par leur probabilité. Les deux variables \(X\) ey \(Y\) sont réduites : du fait du centrage, le nuage est autour de l’origine avec des projections d’espérance nulle, du fait de la normalisation, il est normalement dispersé avec des projections de variance un.
Les deux premiers cas correspondent à une corrélation maximale, avec une relation linéaire. Les deux derniers cas correspondent à une décorrélation : aucune relation linéaire n’est possible. Cependant pour le nuage en triangle, une dépendance est présente : \(\reduc{}\ Y = (\reduc{}\ X)^2 - 1\). Pour le nuage en carré, les variables sont bien indépendantes : connaître la valeur de l’une ne donne aucune information sur l’autre.
Voici des exemples concernant une centaine de points, avec des variables qui ne sont pas réduites et induisent une loi uniforme de probabilité. Le coefficient de corrélation est indiqué à chaque fois, sauf une, où il n’est pas défini, la variable \(Y\) étant nulle.
Parmi les nuages correspondant à une décorrélation (soit de coefficient nul), celui de la première ligne ainsi que celui à l’extrême droite sur la dernière ligne, une variante du nuage en carré de la Figure 3.3, correspondent à des variables indépendantes. C’est la question que nous étudions désormais.
3.1.3 Indépendance de variables aléatoires
AFFAIRE(introduction - cf. Kolmogorov, trait distinctif de la théorie des probabilités, §I.5 Indépendance)
Pour comprendre la notion d’indépendance, construisons un modèle d’expériences aléatoires pour lequel une notion d’indépendance se définit naturellement et simplement, puis montrons le caractère universel de ce modèle, en y interprétant toute expérience aléatoire discrète et tout phénomène associé d’indépendance.
Imaginons comme expérience aléatoire élémentaire le tirage d’une boule colorée contenue dans une urne, l’issue du tirage étant la couleur de la boule. L’urne contient un certain nombre de boules, et si le tirage se fait sans possibilité de discriminer une couleur, la probabilité d’obtenir une couleur devient la proportion de boules de cette couleur dans l’urne. Cette probabilité est un nombre rationnel, et peut donc approcher toute probabilité réelle aussi près qu’on le souhaite, en jouant sur la proportion. À partir de cette expérience aléatoire élémentaire, on peut élaborer une expérience aléatoire complexe10 en répétant les deux opérations suivantes, à réaliser séquentiellement :
- le tirage aléatoire d’une boule,
- la modification des proportions des couleurs, en ajoutant ou retirant des boules suivant un protocole déterministe.
Formellement, le déterminisme se traduit ainsi : la modification après \(n\) expériences aléatoires élémentaires peut être vue comme une fonction associant à chaque séquence de \(n\) issues, soit une séquence de \(n\) couleurs, la nouvelle fonction de probabilité, qui attribue à chaque couleur sa nouvelle proportion dans l’urne. On notera \(\probaCond{c}{S}\) la probabilité de l’issue \(c\) sachant que la séquence des issues précédentes est \(S :\) c’est un exemple de probabilité conditionnelle.
Les expériences aléatoires successives sont dites mutuellement indépendantes si chaque fonction de modification est une fonction constante : elle ne dépend pas de la séquence des issues obtenues précédemment. En revanche les fonctions de modification peuvent varier suivant le nombre d’expériences effectuées. Lorsqu’elles ne varient pas, c’est que le protocole de modification est équivalent à une remise de la boule tirée dans l’urne, si bien que la fonction de probabilité est invariante. C’est un cas évident d’indépendance, mais on peut aussi imaginer des protocoles modifiant les proportions à chaque étape tout en préservant l’indépendance. Si à l’inverse, le protocole consiste à ne rien faire, ce tirage sans remise a pour effet de modifier les proportions des couleurs, donc la fonction de probabilité, qui dépend alors de la séquence des issues : les expériences aléatoires successives ne sont plus indépendantes.
Un arbre pondéré par des probabilités permet de représenter une telle expérience aléatoire complexe. Chaque nœud de l’arbre correspond à une séquence d’issues, à la racine, la séquence vide \(\seqVide{}\), ensuite des séquences non vides d’issues dont la taille augmente d’une unité à chaque transition suivant un arc. Dans la Figure 3.5, deux couleurs \(\blanc{}\) et \(\noir{}\) sont utilisées, et les séquences d’issues sont représentées par des séquences comme \(\blanc{}\blanc{}\blanc{}, \blanc{}\blanc{}\noir{}, \ldots.\)
stateDiagram-v2
direction LR
state "ε" as p0
state "B" as m1
state "N" as m2
state "BB" as m21
state "BN" as m22
state "NB" as m23
state "NN" as m24
state "BBB" as m31
state "BBN" as m32
state "BNB" as m33
state "BNN" as m34
state "NBB" as m35
state "NBN" as m36
state "NNB" as m37
state "NNN" as m38
p0 --> m1: p
p0 --> m2: 1-p
m1 --> m21: q
m1 --> m22: 1-q
m2 --> m23: r
m2 --> m24: 1-r
m21 --> m31: s
m21 --> m32: 1-s
m22 --> m33: t
m22 --> m34: 1-t
m23 --> m35: u
m23 --> m36: 1-u
m24 --> m37: v
m24 --> m38: 1-v
Étant donné une séquence \(S\) d’issues et une issue \(c\), une couleur, \(\blanc{}\) ou \(\noir{}\) dans la Figure 3.5, un arc entre deux nœuds adjacents \(S\) et \(Sc\) est étiquetée par \(\probaCond{c}{S},\) la probabilité d’obtenir une issue \(c\) après la séquence \(S\) d’issues aboutissant au nœud à l’origine de l’arc. Par exemple, dans la Figure 3.5, les probabilités pour obtenir \(\blanc{}\) et \(\noir{}\) après la séquence \(\blanc{}\noir{}\) sont respectivement \(t\) et \(1-t.\) Les probabilités peuvent être placées librement sur les arcs, avec la seule contrainte de normalisation à respecter : la somme des probabilités sur les arcs sortant d’un nœud vaut un, comme dans la Figure 3.5. Ainsi, si on utilise \(r\) couleurs et une séquence de \(n\) expériences aléatoires, il est possible de librement choisir en chaque nœud \(r-1\) réels entre zéro et un, pour obtenir \(r\) intervalles dont la somme fait un, soit au total le choix de \[ (r-1)+r*(r-1)+r^2*(r-1)+\ldots+r^{n-1}*(r-1) \] réels, soit \(r^n - 1\) réels. Dans le cas d’une indépendance entre les expériences, pour chaque expérience, on doit choisir \(r - 1\) réels entre zéro et un pour obtenir les \(r\) probabilités, ce qui donne au total \(n * (r-1)\) réels à choisir.
Intéressons-nous maintenant aux séquences \(S_n\) de longueur \(n\) obtenues en réalisant consécutivement \(n\) expériences aléatoires élémentaires suivant un certain protocole. Comment calculer la probabilité \(\proba{}\ S_n\)11 d’obtenir une séquence particulière \(S_n\) de \(n\) issues ? Elle est égale au nombre total de séquences de \(n\) tirages produisant l’issue \(S_n\) divisé par le nombre total de séquences de \(n\) tirages consécutifs. Ainsi elle est égale au produit des probabilités rencontrées sur le chemin de la racine de l’arbre à la feuille étiquetée par la séquence d’issues, puisque chaque probabilité indique pour une expérience élémentaire le rapport entre le nombre de tirages réalisant l’issue et le nombre total de tirages et que d’une expérience à la suivante, les nombres de tirages possibles se multiplient pour donner le nombre de séquences. On obtient ainsi la définition récursive suivante : \[ \begin{array}{lcl} \proba{}\ \seqVide{} & = & 1,\\ \proba{}\ Sc & = & (\proba{}\ S)*(\probaCond{c}{S}).\\ \end{array} \]
Vérifions que la somme des probabilités obtenues pour toutes les séquences composées de \(n\) issues élémentaires vaut bien un. C’est vérifié au rang un, et si on le suppose au rang \(n,\) c’est vérifié au rang suivant : \[ \begin{array}{rcl} \sum_{S_{n+1}} (\proba{}\ S_{n+1}) &=& \sum_{S_{n}, c} (\proba{}\ S_{n})*(\probaCond{c}{S_n}) \\ &=& \sum_{S_{n}} \sum_c (\proba{}\ S_{n})*(\probaCond{c}{S_n}) \\ &=& \sum_{S_{n}} (\proba{}\ S_{n})*(\sum_c \probaCond{c}{S_n}) & \textrm{(factorisation)}\\ &=& \sum_{S_{n}} (\proba{}\ S_{n})*1 & \textrm{(normalisation)}\\ &=& 1 & \textrm{(hyp. de récurrence).}\\ \end{array} \] Conclusion : par récurrence, pour tout entier naturel \(n\) non nul, \(\sum_{S_{n}} (\proba{}\ S_{n}) = 1.\)
La démonstration repose sur la propriété de normalisation en tout nœud de l’arbre correspondant à une séquence \(S_k :\) \(\sum_{c} \probaCond{c}{S_k} = 1.\) On peut généraliser cette propriété en se plaçant au sous arbre ayant pour racine le nœud de l’arbre étiqueté par la séquence \(S_k\) et en considérant les probabilités conditionnelles \(\probaCond{S_{n-k}}{S_k}\) égales au produit des probabilités rencontrées sur le chemin de la racine du sous-arbre à la feuille étiquetée par la séquence d’issues \(S_k S_{n-k}\). On a alors la propriété de normalisation suivante : \[ \sum_{S_{n-k}} \probaCond{S_{n-k}}{S_k} = 1, \] qui se démontre de la même manière en utilisant la propriété de normalisation élémentaire.
L’expérience aléatoire complexe se décompose naturellement en une séquence d’évènements élémentaires, paramétrés par la couleur \(c\) et la position \(k\) dans la séquence d’expériences : “la \(k\)-ième expérience a pour issue la couleur \(c\)”. Cet évènement peut être interprété comme le prédicat \(\pi_k = c,\) où \(\pi_k\) est la variable aléatoire donnant la \(k\)-ième valeur de la séquence \(S_n,\) autrement dit la \(k\)-ième projection élémentaire. Comme la proposition \(\pi_k\ S_n = c\) est équivalente à l’existence de \(S_{k-1}\) et de \(S_{n-k}\) vérifiant \(S_n = S_{k-1}cS_{n-k},\) nous avons \[ \begin{array}{rcl} \proba{}\ (\pi_k = c) & = & \sum_{S_n\mid \pi_k\ S_n = c} \proba{}\ S_n \\ & = & \sum_{S_{k-1}, S_{n-k}} \proba{}\ S_{k-1}cS_{n-k} \\ & = & \sum_{S_{k-1}, S_{n-k}} (\proba{}\ S_{k-1}c) * (\probaCond{S_{n-k}}{S_{k-1}c}) \\ & = & \sum_{S_{k-1}} \sum_{S_{n-k}} (\proba{}\ S_{k-1}c) * (\probaCond{S_{n-k}}{S_{k-1}c}) \\ & = & \sum_{S_{k-1}} (\proba{}\ S_{k-1}c) * (\sum_{S_{n-k}} \probaCond{S_{n-k}}{S_{k-1}c}) \\ & = & \sum_{S_{k-1}} \proba{}\ S_{k-1}c \\ & = & \sum_{S_{k-1}} (\proba{}\ S_{k-1}) * (\probaCond{c}{S_{k-1}}). \\ \end{array} \]
En cas d’indépendance, la probabilité conditionnelle \(\probaCond{c}{S_{k-1}}\) ne dépend pas de \(S_{k-1}\) et est donc une constante factorisable, si bien que pour toute séquence \(S_{k-1},\) la probabilité conditionnelle \(\probaCond{c}{S_{k-1}}\) est égale à la probabilité \(\proba{}\ (\pi_k = c),\) puisque la somme \(\sum_{S_{k-1}} (\proba{}\ S_{k-1})\) vaut un, par normalisation. Formellement : \[ \forall S_{k-1}, \probaCond{c}{S_{k-1}} = \proba{}\ (\pi_k = c). \] Étant donné \(k\) entre \(1\) et \(n,\) reprenons l’équation récursive fondamentale pour \(S_{k-1} := c_1\ldots c_{k-1}\) et \(c := c_k :\) \[ \proba{}\ c_1\ldots c_{k} = (\proba{}\ c_1\ldots c_{k-1})*(\probaCond{c_k}{c_1\ldots c_{k-1}}). \] d’où la double caractérisation \[ \begin{array}{lcl} \proba{}\ c_1\ldots c_{k} &=& (\proba{}\ c_1\ldots c_{k-1})*(\proba{}\ (\pi_k = c_k))\\ & = & \proba{}\ \bigwedge_{j=1}^k(\pi_j = c_j), \end{array} \] la première égalité découlant d’une récurrence immédiate, la seconde de l’équivalence entre la proposition \(S_k = c_1\ldots c_k\) et la conjonction \((\pi_1 S_n = c_1) \wedge \ldots \wedge (\pi_k S_k = c_k).\)
Ainsi l’indépendance entre les expériences successives se traduit par une propriété remarquable pour les projections successives : les probabilités croisées s’obtiennent par multiplication, ou encore la fonction de probabilité devient un morphisme des conjonctions vers les produits. Cette propriété caractérise l’indépendance mutuelle entre les variables aléatoires \((\pi_k)\), ou entre les systèmes complets d’évènements induits par ces variables.
Avant de passer à la définition formelle, il est utile d’étudier la structure algébrique de l’ensemble des systèmes complets d’évènements.
AFFAIRE(déf formelle en \(n,\) car déduit en $k n.$0)
Proposition 3.7 (Monoïde commutatif et idempotent) L’ensemble des systèmes complets d’évènements forme un monoïde AFFAIRE(lien vers cours) pour l’intersection ainsi définie : \[ \partition{E_j}{j\in J} \cap \partition{F_k}{k\in K} = \partition{E_j \cap F_k}{(j, k) \in J\times K}. \]
Son élément neutre est \(\{\Univ{}\}\). L’intersection est commutative et idempotente.
- Commutativité : \(\forall \partition{E_j}{j}, \partition{F_k}{k}, \partition{E_j}{j} \cap \partition{F_k}{k} = \partition{F_k}{k} \cap \partition{E_j}{j}.\)
- Idempotence : \(\forall \partition{E_j}{j}, \partition{E_j}{j} \cap \partition{E_j}{j} = \partition{E_j}{j}.\)
Il est aussi possible d’ordonner les systèmes complets d’évènements par une forme d’inclusion.
Proposition 3.8 (Ordre entre systèmes complets d’évènements) Définissons une relation \(\pFine{}\) entre les systèmes complets d’évènements : le système \(\partition{E_j}{j\in J}\) raffine \(\partition{F_k}{k\in K},\) noté \(\partition{E_j}{j\in J} \pFine{} \partition{F_k}{k\in K},\) s’il existe une fonction \(\fctn{\iota}{J}{K}\) telle que pour tout \(k\in K\) tel que \(F_k\), la famille \(\partition{E_j}{j\in \iterOp{\iota}{\circ}{-1}\ k}\) forme une partition de \(F_k.\)
La relation \(\pFine{}\) définit un ordre partiel : elle est réflexive, anti-symétrique et transitive.
Définition 3.4 (Indépendance mutuelle) Considérons une famille \((\partition{E_{j, k}}{j})_{k=1}^n\) formée de \(n\) systèmes complets d’évènements \(\partition{E_{j, k}}{j}.\) Alors les systèmes \((\partition{E_{j, k}}{j})_k\) sont mutuellement indépendants si les probabilités croisées s’obtiennent par multiplication : \[ \forall (j_1\ \ldots\ j_n), \proba{}\ \bigcap_{k=1}^n E_{j_k, k} = \prod_{k=1}^n \proba{}\ E_{j_k, k}. \]
Considérons une famille \((\fctn{X_k}{\Univ{}}{A_k})_{k=1}^n\) de variables aléatoires. Alors les variables aléatoires \((X_k)_k\) sont mutuellement indépendantes si les probabilités croisées s’obtiennent par multiplication : \[ \forall (c_1\in A_1)\ldots (c_n\in A_n), \proba{}\ \bigcap_{k=1}^n (X_k = c_k) = \prod_{k=1}^n \proba{}\ (X_k = c_k). \]
L’indépendance mutuelle est préservée par restriction à une sous-famille.
Proposition 3.9 (Préservation de l’indépendance mutuelle par restriction) Soit \((\partition{E_{j, k}}{j})_{k=1}^n\) une famille formée de \(n\) systèmes complets d’évènements \(\partition{E_{j, k}}{j}\) mutuellement indépendants. Alors pour tout entier naturel non nul \(m\) inférieur ou égal à \(n\), les systèmes \((\partition{E_{j, k}}{j})_{k=1}^m\) sont mutuellement indépendants.
Grâce à la formalisation par des évènements ou des variables aléatoires, la Définition 3.4 généralise donc celle rencontrée dans notre modèle d’expérience aléatoire complexe, définition qui se comprend bien intuitivement puisqu’elle repose sur l’indépendance entre les expériences successives. Inversement, nous montrons que toute expérience aléatoire accompagnée d’une famille de systèmes complets d’évènements peut être modélisée par une expérience aléatoire complexe utilisant des urnes et que les notions d’indépendance coïncident.
Considérons une famille \(((E_{j, k})_j)_{k=1}^n\) formée de \(n\) systèmes complets d’évènements \((E_{j, k})_j.\) Construisons un arbre pondéré par des probabilités :
- chaque nœud de rang \(m\) est étiqueté par une intersection \(E_{j_1, 1}\cap\ldots\cap E_{j_m, m}\) de \(m\) évènements, un par système complet \((E_{j, k})_j,\) pour \(k\) entre \(1\) et \(m,\)
- un arc réalisant la transition de \(E_{j_1, 1}\cap\ldots\cap E_{j_m, m}\) à \(E_{j_1, 1}\cap\ldots \cap E_{j_m, m}\cap E_{j_{m+1}, m+1}\) est étiqueté par la probabilité conditionnelle \(\probaCond{E_{j_{m+1}, m+1}}{E_{j_1, 1}\cap\ldots\cap E_{j_m, m}},\) égale au rapport \(\proba{}\ E_{j_1, 1}\cap\ldots \cap E_{j_m, m}\cap E_{j_{m+1}, m+1}/\proba{}\ E_{j_1, 1}\cap\ldots\cap E_{j_m, m}.\)
Cet arbre vérifie bien la propriété fondamentale des arbres pondérés par des probabilités : la somme des probabilités étiquetant les arcs sortant d’un nœud vaut \(1,\) puisque les systèmes sont complets. Il est ainsi possible de réaliser une expérience aléatoire complexe dont la représentation arborescente est exactement le même arbre pondéré, ou s’en approche aussi près qu’on le souhaite. L’indépendance des systèmes complets d’évènements implique que les expériences aléatoires successives du modèle sont bien indépendantes, puisque par la Proposition 3.9 chaque probabilité conditionnelle \(\probaCond{E_{j_{m+1}, m+1}}{E_{j_1, 1}\cap\ldots\cap E_{j_m, m}}\) se simplifie en \(\proba{}\ E_{j_{m+1}, m+1}.\) Réciproquement, si les expériences aléatoires successives du modèle sont indépendantes, alors les systèmes complets d’évènements sont mutuellement indépendants. C’est un corollaire de la proposition suivante, précisément de l’implication de (C) à (A), dont la démonstration suit celle ayant abouti à l’?eq-independanceModele.
Proposition 3.10 (Indépendance mutuelle : équivalences) Soit \(((E_{j, k})_j)_{k=1}^n\) une famille formée de \(n\) systèmes complets d’évènements \((E_{j, k})_j.\) Alors les propositions suivantes sont équivalentes.
- Les systèmes complets d’évènements \(((E_{j, k})_j)_{k=1}^n\) sont mutuellement indépendants.
- Pour tout entier naturel \(m\) non nul inférieur ou égal à \(n\), les systèmes complets d’évènements \(((E_{j, k})_j)_{k=1}^m\) sont mutuellement indépendants.
- Pour tout entier naturel non nul \(m\) inférieur strictement à \(n\), les deux systèmes complets d’évènements $(E_{j, m})_j et \(\bigcap_{k=1}^{m-1} (E_{j, k})_j\) sont mutuellement indépendants.
AFFAIRE(
- inversement, interprétation d’une expérience aléatoire dans ce modèle universel
- généralisation à \(n\) partitions (ou \(n\) variables aléatoires)
- construction via arbre pondéré
- interprétation par un tableau, probabilités marginales
- question de l’ordre à régler, 1 tableau -> n! arbres mais choix indifférent de la permutation
)
- question de l’ordre à régler, 1 tableau -> n! arbres mais choix indifférent de la permutation
AFFAIRE(suite à voir - cf. texte dans brouillon)
L’indépendance est préservée par réunion des parties de chaque partition.
Proposition 3.11 (Partitions indépendantes : préservation de l’indépendance par union AFFAIRE(coalition)) Soient \((A_i)_i\) et \((B_j)_i\) deux partitions indépendantes. Alors toute union \(\bigcup_{i\in I} A_i\) de parties de la partition \((A_i)_i\) et toute union \(\bigcup_{j\in J} B_j\) de parties de la partition \((B_j)_i\) sont indépendantes.
Comme toute variable aléatoire induit par la décomposition canonique une partition des issues, on peut définir l’indépendance de deux variables aléatoires par l’indépendance des partitions induites.
Définition 3.5 (Indépendance entre variables aléatoires) Soient \(\fctn{X_1}{\Univ{}}{A_1}\) et \(\fctn{X_2}{\Univ{}}{A_2}\) deux variables aléatoires vers \(A_1\) et \(A_2\) respectivement. Les variables aléatoires \(X_1\) et \(X_2\) sont indépendantes si pour tout couple \((v_1, v_2)\) appartenant à \(A_1 \times A_2\), les évènements \(X_1 = v_1\) et \(X_2 = v_2\) sont indépendants : \[ \proba{}\ ((X_1 = v_1) \wedge (X_2 = v_2)) = (\proba{}\ (X_1 = v_1)) * (\proba{}\ (X_2 = v_2)). \]
L’indépendance permet de simplifier l’espérance du produit de deux variables aléatoires (leur produit scalaire), ainsi que la variance d’une somme, qui deviennent alors des morphismes.
Proposition 3.12 (Espérance d’un produit de variables aléatoires numériques indépendantes) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) deux variables aléatoires numériques indépendantes. Alors l’espérance de leur produit est égale au produit de leurs espérances : \[ \esper{}\ (X * Y) = (\esper{}\ X) * (\esper{}\ Y). \]
Corollaire 3.4 (Variance d’une somme de variables aléatoires numériques indépendantes) Soient \(\fctn{X}{\Univ{}}{\Reel{}}\) et \(\fctn{Y}{\Univ{}}{\Reel{}}\) deux variables aléatoires numériques indépendantes. Alors la variance de leur somme est égale à la somme de leurs variances : \[ \variance{}\ (X + Y) = (\variance{}\ X) + (\variance{}\ Y). \]
Comment construire des variables aléatoires indépendantes ? Il est possible de produire deux variables aléatoires indépendantes à partir de deux variables aléatoires quelconques \(\fctn{X_1}{\Univ{}_1}{A_1}\) et \(\fctn{X_2}{\Univ{}_2}{A_2},\) sans même supposer qu’elles soient définies sur le même univers. En effet, concrètement il suffit de réaliser les deux expériences aléatoires associées à \(X_1\) et \(X_2\), de manière indépendante. Formellement, l’univers devient le produit cartésien \(\Univ{}_1 \times \Univ{}_2\), et si \(\proba{}_1\) et \(\proba{}_2\) sont les fonctions de probabilités sur \(\Univ{}_1\) et \(\Univ{}_2\) respectivement, alors la fonction de probabilité \(\proba{}\) est définie sur \(\Univ{}_1 \times \Univ{}_2\) par \(\proba{}\ (i_1, i_2) := (\proba{}_1\ i_1) * (\proba{}_2\ i_2),\) ce qui exprime l’indépendance. Cette propriété s’étend au produit cartésien de deux évènements \(E_1 \subseteq \Univ{}_1\) et \(E_2 \subseteq \Univ{}_2 :\) : \(\proba{}\ (E_1 \times E_2) = (\proba{}_1\ E_1) * (\proba{}_2\ E_2).\) En effet : \[ \begin{array}{rcl} \proba{}\ (E_1 \times E_2) & = & \sum_{(i_1, i_2)\in E_1 \times E_2} \proba{}\ (i_1, i_2) \\ & = & \sum_{(i_1, i_2)\in E_1 \times E_2} (\proba{}_1\ i_1) * (\proba{}_2\ i_2) \\ & = & (\sum_{i_1\in E_1} (\proba{}_1\ i_1)) * (\sum_{i_2\in E_2} (\proba{}_2\ i_2)) \\ & = & (\proba{}_1\ E_1) * (\proba{}_2\ E_2). \end{array} \]
Sur ce nouvel univers, définissons deux variables aléatoires \(\fctn{X'_1}{\Univ{}_1 \times \Univ{}_2}{A_1}\) et \(\fctn{X'_2}{\Univ{}_1\times \Univ{}_2}{A_2},\) par \(X'_1\ (i_1, i_2) := X_1\ i_1\) et \(X'_2\ (i_1, i_2) := X_2\ i_2.\)
Quelles sont les probabilités induites par ces variables aléatoires ? Soit \(v\) dans \(A_1.\) L’ensemble \(\{(i_1, i_2)\in \Univ{}_1 \times \Univ{}_2 \mid X'_1\ (i_1, i_2) = v \}\) est égal à \((X_1^{-1}\ \{v\})\times \Univ{}_2,\) qui a pour probabilité \(\proba{}_1\ (X_1 = v).\) Ainsi, la loi de probabilité associée à \(X'_1\) est identique à celle associée à \(X_1\) et de même pour \(X'_2\). Montrons finalement que les variables aléatoires \(X'_1\) et \(X'_2\) sont indépendantes. \[ \begin{array}{rcl} ((X'_1 = v_1) \wedge (X'_2 = v_2)) &=& \{(i_1, i_2)\in \Univ{}_1 \times \Univ{}_2 \mid X'_1\ (i_1, i_2) = v_1 \wedge X'_2\ (i_1, i_2) = v_2 \}\\ &=& \{(i_1, i_2)\in \Univ{}_1 \times \Univ{}_2 \mid X_1\ i_1 = v_1 \wedge X_2\ i_2 = v_2 \}\\ &=& (X_1 = v_1) \times (X_2 = v_2). \\ \end{array} \] Ainsi \(\proba{}\ ((X'_1 = v_1) \wedge (X'_2 = v_2)) = (\proba{}_1\ (X_1 = v_1)) * (\proba{}_2\ (X_2 = v_2)).\) Comme \(X_1\) et \(X'_2\) ont la même loi de probabilité, comme \(X_2\) et \(X'_2,\) on en déduit l’indépendance : \[ \proba{}\ ((X'_1 = v_1) \wedge (X'_2 = v_2)) = (\proba{}\ (X'_1 = v_1)) * (\proba{}\ (X'_2 = v_2)). \]
Cette construction est fréquemment utilisée pour répéter \(n\) fois une expérience aléatoire. Étant donné une variable aléatoire \(\fctn{X}{\Univ{}}{A}\) associée à l’expérience aléatoire, on définit alors \(n\) variables aléatoires \(\fctn{X \ circ \pi_k}{\Univ{}^n}{A}\), où \(\pi_k\) est la \(k\)-ième projection. Ces variables aléatoires sont indépendantes et de même loi que \(X\). Cette construction mène à la notion d’échantillon.
Définition 3.6 (Échantillon) Un échantillon de taille \(n\) est une séquence de \(n\) variables aléatoires \((\fctn{X_k}{\Univ{}}{A})_k\) indépendantes et partageant la même loi de probabilité12. L’échantillon a pour somme la variable aléatoire \(\sum_{k=1}^{n} X_k\) et pour moyenne la variable aléatoire \((\sum_{k=1}^{n} X_k)/n\).
Grâce aux propriétés de linéarité (Proposition 3.4) et à l’indépendance (Corollaire 3.4), il est possible de calculer l’espérance et la variance de la somme et de la moyenne d’un échantillon.
AFFAIRE(
- échantillon
- espérance/variance somme/moyenne
- loi de concentration (inégalité de Tcheby)000
- loi faible des grands nombres à la limite
- sens
- pourquoi faible ? lois fortes avec convergence plus forte.
)
3.1.4 Encadrement des probabilités d’appartenance à un intervalle
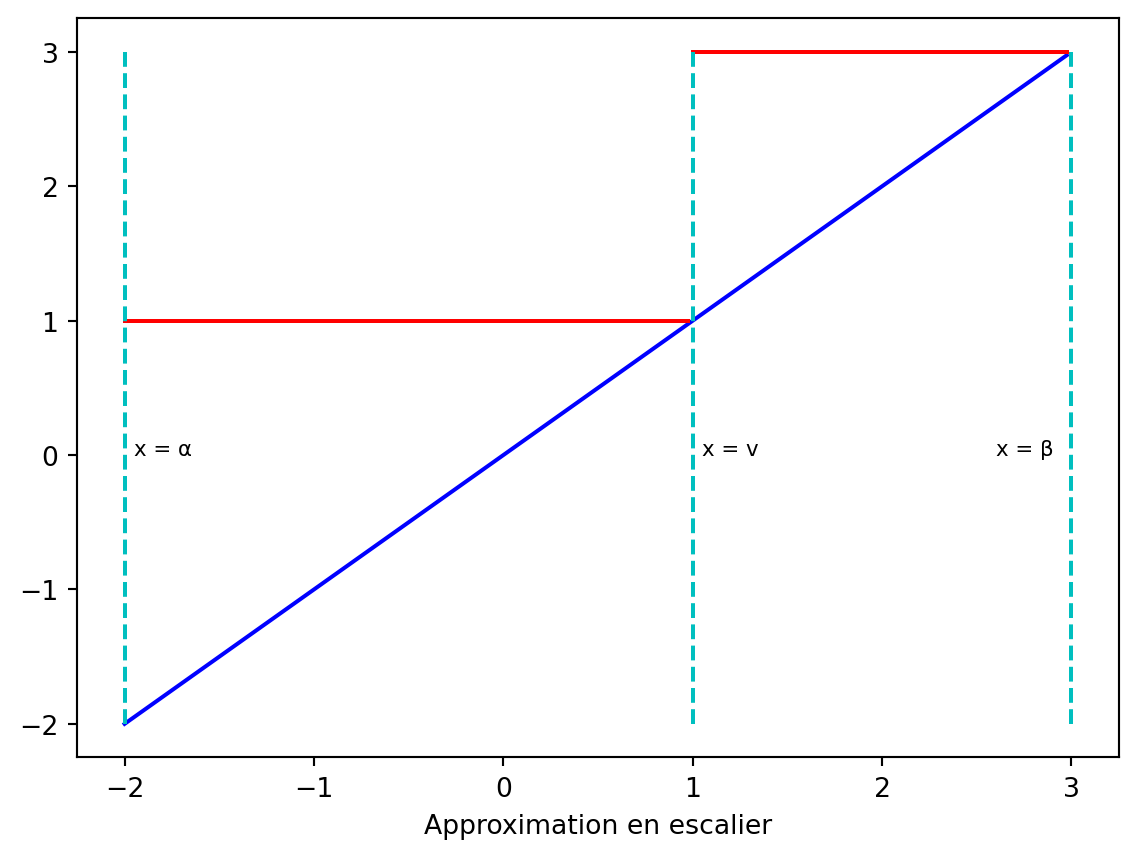
Il peut être intéressant de considérer un intervalle de la forme \(\croD{}v_1, v_2\croG{}, \croD{}v_1, +\infty\croD{}\) ou \(\croG{}-\infty, v_2\croG{}\) pour les valeurs possibles d’une variable aléatoire numérique \(X\) et d’encadrer la probabilité de l’appartenance à l’intervalle, \(\proba{}\ (v_1 \leq X \leq v_2), \proba{}\ (v_1 \leq X)\) ou \(\proba{}\ (X \leq v_2).\) Comme l’évènement \(v_1 \leq X \leq v_2\) correspond à l’évènement \((X - (v_1 + v_2)/2)^2 \leq ((v_2 - v_1)/2)^2\) en majorant la distance au centre de l’intervalle par la moitié de la longueur de l’intervalle, il est possible de se limiter aux évènements \(X \leq v_2\) et \(X^2 \leq v^2_2,\) ainsi que \(v_1 \leq X\) et \(v^2_1 \leq X^2.\)
Pour encadrer leur probabilité, l’idée est d’encadrer un moment en décomposant suivant les évènements complémentaires d’appartenance ou non à l’intervalle considéré, par exemple \(X \leq v\) et \(X > v\).
Moment d’ordre \(k\), avec \(k\) impair – Soient \(\alpha\) et \(\beta\) deux réels minorant et majorant presque sûrement \(X :\) \[ \proba{}\ (\alpha \leq X \leq \beta) = 1. \]
Soit \(v_2\) un réel. Comme la probabilité \(\proba{}\ (X \leq v_2)\) vaut \(1\) lorsque \(v_2 \geq \beta,\) intéressons-nous au seul cas \(v_2 < \beta\). Définissons une variable aléatoire \(B\) ainsi : \[ B\ i = \left\{\begin{array}{l} v_2 \textrm{ si } X\ i \leq v_2, \\ \beta \textrm{ si } X\ i > v_2. \\ \end{array} \right. \]
Comme \(B\) majore presque sûrement \(X\), on a par croissance \(\moment{}_{k}\ X \leq \moment{}_{k}\ B,\) ce qui donne
\[
\begin{array}{rcl}
\moment{}_{k}\ X & \leq & v_2^k * (\proba{}\ (X \leq v_2)) + \beta^k * (\proba{}\ (X > v_2)) \\
&\leq& (\proba{}\ (X \leq v_2)) * (v_2^k - \beta^k) + \beta^k, \\
\proba{}\ (X \leq v_2) &\leq &
(\beta^k - (\moment{}_{k}\ X))/(\beta^k - v_2^k).
\end{array}
\] Le majorant n’est pertinent que s’il est inférieur à \(1\), soit si \(v_2^k < \moment{}_{k}\ X.\) Par complémentarité, on obtient : \[
\begin{array}{rcl}
\proba{}\ (X > v_2) &\geq & 1 - (\beta^k - (\moment{}_{k}\ X))/(\beta^k - v_2^k)\\
&\geq& ((\moment{}_{k}\ X) - v_2^k)/(\beta^k - v_2^k). \\
\end{array}
\]
Symétriquement, soit \(v_1\) un réel. Comme la probabilité \(\proba{}\ (X \geq v_1)\) vaut \(1\) lorsque \(v_1 \leq \alpha,\) intéressons-nous au seul cas \(v_1 > \alpha\). Définissons une variable aléatoire \(A\) ainsi : \[ A\ i = \left\{\begin{array}{l} v_1 \textrm{ si } X\ i \geq v_1, \\ \alpha \textrm{ si } X\ i < v_1. \\ \end{array} \right. \]
Comme \(A\) minore presque sûrement \(X\), on a par croissance \(\moment{}_{k}\ X \geq \moment{}_{k}\ A,\) ce qui donne
\[
\begin{array}{rcl}
\moment{}_{k}\ X & \geq & v_1^k * (\proba{}\ (X \geq v_1)) + \alpha^k * (\proba{}\ (X < v_1)) \\
&\geq& (\proba{}\ (X \geq v_1)) * (v_1^k - \alpha^k) + \alpha^k, \\
\proba{}\ (X \geq v_1) &\leq &
((\moment{}_{k}\ X) - \alpha^k)/(v_1^k - \alpha^k). \\
\end{array}
\] Le majorant n’est pertinent que s’il est inférieur à \(1\), soit si \(v_1^k > (\moment{}_{k}\ X).\) Par complémentarité, on obtient : \[
\begin{array}{rcl}
\proba{}\ (X < v_1) &\geq & 1 - ((\moment{}_{k}\ X) - \alpha^k)/(v_1^k - \alpha^k) \\
& \geq & (v_1^k - (\moment{}_{k}\ X))/(v_1^k - \alpha^k). \\
\end{array}
\]
Moment d’ordre \(k\), avec \(k\) pair – Soient \(\alpha\) et \(\beta\) deux réels positifs dont les carrés minorent et majorent presque sûrement \(X^2 :\) \[ \proba{}\ (\alpha^2 \leq X^2 \leq \beta^2) = 1. \]
Soit \(v_2\) un réel positif. Comme la probabilité \(\proba{}\ (X^2 \leq v^2_2)\) vaut \(1\) lorsque \(v_2^2 \geq \beta^2,\) intéressons-nous au seul cas \(v_2^2 < \beta^2\). Définissons une variable aléatoire \(B\) ainsi : \[ B\ i = \left\{\begin{array}{l} v_2 \textrm{ si } X^2\ i \leq v^2_2, \\ \beta \textrm{ si } X^2\ i > v^2_2. \\ \end{array} \right. \]
Comme \(B^2\) majore presque sûrement \(X^2\), on a par croissance \(\moment{}_{k}\ X \leq \moment{}_{k}\ B,\) ce qui donne
\[
\begin{array}{rcl}
\moment{}_{k}\ X & \leq & v_2^k * (\proba{}\ (X^2 \leq v^2_2)) + \beta^k * (\proba{}\ (X^2 > v^2_2)) \\
&\leq& (\proba{}\ (X^2 \leq v^2_2)) * (v_2^k - \beta^k) + \beta^k, \\
\proba{}\ (X^2 \leq v^2_2) &\leq &
(\beta^k - (\moment{}_{k}\ X))/(\beta^k - v_2^k).
\end{array}
\] Le majorant n’est pertinent que s’il est inférieur à \(1\), soit si \(v_2^k < \moment{}_{k}\ X.\) Par complémentarité, on obtient : \[
\begin{array}{rcl}
\proba{}\ (X^2 > v^2_2) &\geq & 1 - (\beta^k - (\moment{}_{k}\ X))/(\beta^k - v_2^k)\\
&\geq& ((\moment{}_{k}\ X) - v_2^k)/(\beta^k - v_2^k). \\
\end{array}
\]
Symétriquement, soit \(v_1\) un réel positif. Comme la probabilité \(\proba{}\ (X^2 \geq v^2_1)\) vaut \(1\) lorsque \(v^2_1 \leq \alpha^2,\) intéressons-nous au seul cas \(v^2_1 > \alpha^2\). Définissons une variable aléatoire \(A\) ainsi : \[ A\ i = \left\{\begin{array}{l} v_1 \textrm{ si } X^2\ i \geq v^2_1, \\ \alpha \textrm{ si } X^2\ i < v^2_1. \\ \end{array} \right. \]
Comme \(A^2\) minore presque sûrement \(X^2\), on a par croissance \(\moment{}_{k}\ X \geq \moment{}_{k}\ A,\) ce qui donne
\[
\begin{array}{rcl}
\moment{}_{k}\ X & \geq & v_1^k * (\proba{}\ (X^2 \geq v^2_1)) + \alpha^k * (\proba{}\ (X^2 < v^2_1)) \\
&\geq& (\proba{}\ (X^2 \geq v^2_1)) * (v_1^k - \alpha^k) + \alpha^k, \\
\proba{}\ (X^2 \geq v^2_1) &\leq &
((\moment{}_{k}\ X) - \alpha^k)/(v_1^k - \alpha^k). \\
\end{array}
\] Le majorant n’est pertinent que s’il est inférieur à \(1\), soit si \(v_1^k > (\moment{}_{k}\ X).\) Par complémentarité, on obtient : \[
\begin{array}{rcl}
\proba{}\ (X^2 < v^2_1) &\geq & 1 - ((\moment{}_{k}\ X) - \alpha^k)/(v_1^k - \alpha^k) \\
& \geq & (v_1^k - (\moment{}_{k}\ X))/(v_1^k - \alpha^k). \\
\end{array}
\]
Récapitulons.
Proposition 3.13 (Encadrement des probabilités d’appartenance à un intervalle) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire.
- Supposons que \(\alpha\) et \(\beta\) soient deux réels minorant et majorant presque sûrement \(X.\) Alors pour tout entier naturel \(k\) impair et pour tout réel \(v\) vérifiant \(\alpha <v < \beta,\) on a : \[ \begin{array}{rcl} \proba{}\ (X \leq v) &\leq & (\beta^k - (\moment{}_{k}\ X))/(\beta^k - v^k) \textrm{ si } v^k \leq (\moment{}_{k}\ X), \\ &\geq & (v^k - (\moment{}_{k}\ X))/(v^k - \alpha^k) \textrm{ si } v^k > (\moment{}_{k}\ X), \\ \proba{}\ (X \geq v) &\geq & ((\moment{}_{k}\ X) - v^k)/(\beta^k - v^k) \textrm{ si } v^k < (\moment{}_{k}\ X), \\ &\leq & ((\moment{}_{k}\ X) - \alpha^k)/(v^k - \alpha^k) \textrm{ si } v^k \geq (\moment{}_{k}\ X). \\ \end{array} \]
- Supposons que \(\alpha\) et \(\beta\) soient deux réels positifs dont les carrés minorent et majorent presque sûrement \(X^2.\) Alors pour tout entier naturel \(k\) pair et pour tout réel \(v\) vérifiant \(\alpha^2 <v^2 < \beta^2,\) on a : \[ \begin{array}{rcl} \proba{}\ (X^2 \leq v^2) &\leq & (\beta^k - (\moment{}_{k}\ X))/(\beta^k - v^k) \textrm{ si } v^k \leq (\moment{}_{k}\ X), \\ &\geq & (v^k - (\moment{}_{k}\ X))/(v^k - \alpha^k) \textrm{ si } v^k > (\moment{}_{k}\ X), \\ \proba{}\ (X^2 \geq v^2) &\geq & ((\moment{}_{k}\ X) - v^k)/(\beta^k - v^k) \textrm{ si } v^k < (\moment{}_{k}\ X), \\ &\leq & ((\moment{}_{k}\ X) - \alpha^k)/(v^k - \alpha^k) \textrm{ si } v^k \geq (\moment{}_{k}\ X). \\ \end{array} \]
Démonstration alternative à partir des valeurs aléatoires
Plutôt que de raisonner à partir des issues et de leurs probabilités originales, on peut directement raisonner à partir des valeurs aléatoires prises par \(X\) et de leurs probabilités induites. Démontrons la première inégalité, les autres se démontrant suivant la même méthode.
Décomposons \(X\ \Univ{}\) en \(\{x \in X\ \Univ{} \mid x > v \}\) et \(\{x \in X\ \Univ{} \mid x \leq v \}\). Définissons une nouvelle variable aléatoire \(\fctn{Y}{X\ \Univ{}}{\Reel{}}\) par \[ Y\ x = \left\{\begin{array}{l} v \textrm{ si } x \leq v, \\ \beta \textrm{ si } x > v. \\ \end{array} \right. \] C’est une fonction en escalier qui majore presque sûrement l’identité, \(\fctn{\idF{}}{X\ \Univ{}}{\Reel{}},\) définie par \(\idF{}\ x = x.\) On déduit par croissance que \(\moment{}_k\ \idF{} \leq \moment{}_k\ Y.\) Pour conclure, observons que \(\moment{}_k\ \idF{} = \moment{}_k\ X,\) ce qui donne \(\moment{}_k\ X \leq \moment{}_k\ Y,\) qui est l’inégalité recherchée.
Code
import math
import numpy as np
import matplotlib.pyplot as plt
def identite(x) :
return x
alpha = -2
beta = 3
v = 1
def marche1(x) :
return v
def marche2(x) :
return beta
tid = np.arange(alpha, beta, 0.025)
plt.plot(tid, list(map(identite, tid)), 'b')
t1 = np.arange(alpha, v, 0.025)
plt.plot(t1, list(map(marche1, t1)), 'r')
t2 = np.arange(v, beta, 0.025)
plt.plot(t2, list(map(marche2, t2)), 'r')
plt.plot([alpha, alpha], [alpha, beta], 'c--')
plt.plot([v, v], [alpha, beta], 'c--')
plt.plot([beta, beta], [alpha, beta], 'c--')
plt.xlabel('Approximation en escalier')
plt.text(alpha+0.05, 0, 'x = α', fontsize=8, color='black')
plt.text(v+0.05, 0, 'x = v', fontsize=8, color='black')
plt.text(beta-0.4, 0, 'x = β', fontsize=8, color='black')
plt.show()
On peut appliquer ces encadrements à l’espérance et à la variance.
Corollaire 3.5 (Inégalité de Markov) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Alors pour tout réel \(v\) strictement supérieur à \(\esper{}\ |X|\) : \[ \proba{}\ (|X| \geq v) \leq (\esper{}\ |X|)/v. \]
Corollaire 3.6 (Inégalité de Bienaimé-Tchebychev) Soit \(\fctn{X}{\Univ{}}{\Reel{}}\) une variable aléatoire. Alors pour tout réel \(v\) strictement supérieur à l’écart-type de \(X\), \(\ecartT{} \ X :\) \[ \proba{}\ (|X - (\esper{}\ X)| \geq v) \leq (\ecartT{}\ X)^2/v^2. \]
Proposition 3.14 (AFFAIRE)
3.2 Loi binomiale
Simulation
from random import *
import matplotlib.pyplot as plt
import numpy as np
# Épreuve de Bernoulli binaire :
# - paramètre p : probabilité de succès
# - renvoie True avec une probabilité p
# - renvoie False avec une probabilité (1-p)
# Documentation pour random : voir https://docs.python.org/fr/3/library/random.html
# - random : fonction aléatoire dans l'intervalle [0, 1] des réels flottants.
# - La fonction X : [0, 1] -> {True, False} définie par X(r) = (r < p) est une variable aléatoire
# qui permet d'obtenir une distribution de probabilité (p, 1-p) sur {True, False}.
# - La fonction aléatoire aleaBinaire est égale à la composée de random avec X : X o random.
def aleaBinaire(p) :
return (random() < p);
# Variable aléatoire comptant le nombre de succès dans un schéma de Bernoulli
# - paramètre n : nombre d'épreuves de Bernoulli
# - paramètre p : probabilité de succès
# - renvoie le nombre de succès
def compteSuccesSchemaBernoulli(n, p) :
s = 0
for i in range(n):
if(aleaBinaire(p)):
s = s + 1
return s
# Simulation de la loi binomiale pour un schéma de Bernoulli
# - paramètre n : nombre d'épreuves de Bernoulli
# - paramètre p : probabilité de succès
# - paramètre nombreSimulations : nombre de simulations du schéma de Bernoulli
# - renvoie un tableau de (n+1) fréquences, indiquant
# pour chaque nombre possible de succès, sa fréquence statistique relative
def simulationLoiBinomiale(n, p, nombreSimulations) :
frequences = [0]*(n + 1) # fréquences à 0 pour les n+1 valeurs possibles du nombre de succès
for i in range(nombreSimulations):
s = compteSuccesSchemaBernoulli(n, p)
frequences[s] = frequences[s] + 1
# passage des fréquences absolues aux fréquences relatives
return list(map(lambda s : s/nombreSimulations, frequences))
# Fonction permettant de calculer le cumul des éléments d'un tableau.
def cumul(tableau) :
n = len(tableau)
s = list(tableau)
for i in range(1, n) :
s[i] = s[i] + s[i-1]
return s
# Fonction calculant la moyenne des valeurs 0, ..., n pondérées
# par la liste passée en argument
# Documentation de dot : https://numpy.org/doc/stable/reference/generated/numpy.dot.html
# - Cette fonction calcule le produit scalaire de deux vecteurs : ici elle donne la moyenne pondérée.
def moyenne(frequencesRelatives) :
taille = len(frequencesRelatives)
valeurs = list(range(0, taille))
return np.dot(frequencesRelatives, valeurs)
# tests de la fonction
nombreEpreuves = 10
probabiliteSucces = 1.0/6.0
nombreSimulations = 100000
frequences = simulationLoiBinomiale(nombreEpreuves, probabiliteSucces, nombreSimulations)
print("* Schéma de bernoulli " + str(nombreEpreuves) + ", " + str(probabiliteSucces))
print("** Simulation par " + str(nombreSimulations) + " expériences : ")
print(" - fréquences relatives des succès : " + str(frequences))
print(" - moyenne des succès : " + str(moyenne(frequences)))
print(" - espérance des succès : " + str(nombreEpreuves * probabiliteSucces))
frequencesCumulatives = cumul(frequences)
plt.style.use('_mpl-gallery')
# données de fréquences:
x = np.arange(0, nombreEpreuves + 1, 1)
y = frequences
# graphique
fig, ax = plt.subplots()
ax.bar(x, y, width=1, edgecolor="white", linewidth=0.7)
ax.set(xticks=np.arange(0, nombreEpreuves + 1, 1), yticks=np.arange(0, max(frequences) + 0.1, 0.1))
plt.show()
# données de cumuls de fréquences
xs = np.arange(0, nombreEpreuves + 1, 1)
ys = frequencesCumulatives
# graphique
fig, ax = plt.subplots()
ax.bar(xs, ys, width=1, edgecolor="white", linewidth=0.7)
ax.set(xticks=np.arange(0, nombreEpreuves + 1, 1), yticks=np.arange(0, 1 + 0.1, 0.1))
plt.show()* Schéma de bernoulli 10, 0.16666666666666666
** Simulation par 100000 expériences :
- fréquences relatives des succès : [0.16273, 0.32279, 0.29003, 0.15439, 0.05493, 0.01272, 0.00213, 0.00025, 3e-05, 0.0, 0.0]
- moyenne des succès : 1.66411
- espérance des succès : 1.6666666666666665
3.3 Annales
3.3.1 Bac 2024
Un jeu vidéo récompense par un objet tiré au sort les joueurs ayant remporté un défi. L’objet tiré peut être “commun” ou “rare”. Deux types d’objets commun ou rare sont disponibles, des épées ou des boucliers.
Les concepteurs du jeu vidéo ont prévu que :
- la probabilité de tirer un objet rare est de \(7\%\) ;
- si on tire un objet rare, la probabilité que ce soit une épée est de \(80\%\) ;
- si on tire un objet commun, la probabilité que ce soit une épée est de \(40\%\).
Les parties A et B sont indépendantes.
3.3.1.1 Partie A
Un joueur vient de remporter un défi et tire au sort un objet . On note :
- \(R\) l’événement “le joueur tire un objet rare” ;
- \(E\) l’événement “le joueur tire une épée” ;
- \(\bar{R}\) et \(\bar{E}\) sont les événements contraires de \(R\) et \(E\).
- Dresser un arbre pondéré modélisant la situation, puis calculer \(P(R \cap E)\).
- Calculer la probabilité de tirer une épée.
- Le joueur a tiré une épée. Déterminer la probabilité que ce soit un objet rare. Arrondir le résultat au millième.
3.3.1.2 Partie B
Un joueur remporte \(30\) défis. On note \(X\) la variable aléatoire correspondant au nombre d’objets rares que le joueur obtient après avoir remporté \(30\) défis. Les tirages successifs sont considérés comme indépendants.
- Déterminer, en justifiant, la loi de probabilité suivie par la variable \(X\). Préciser ses paramètres et son espérance.
- Déterminer \(P(X < 6)\). Arrondir le résultat au millième.
- Déterminer la plus grande valeur de \(k\) telle que \(P(X \geq k) \geq 0,5\). Interpréter le résultat dans le contexte de l’exercice.
- Les développeurs du jeu vidéo, veulent proposer aux joueurs d’acheter un “ticket d’or” qui permet de tirer \(N\) objets. La probabilité de tirer un objet rare reste de \(7\%\). Les développeurs aimeraient qu’en achetant un ticket d’or, la probabilité qu’un joueur obtienne au moins un objet rare lors de ces \(N\) tirages soit supérieure ou égale à \(0,95\). Déterminer le nombre minimum d’objets à tirer pour atteindre cet objectif. On veillera à détailler la démarche mise en place.
Issue : ce qui sort. On dit aussi “résultat” ou “possibilité”.↩︎
Algèbre de Boole : ensemble à deux éléments, le vrai et le faux.↩︎
On peut le négliger, faire comme s’il n’existait pas. On pourrait dire chimérique : qui n’a aucune chance de se réaliser. Le qualificatif impossible est plus usité mais laisse entendre que l’évènement ne peut pas se produire. Ne jamais sortir de six en jouant indéfiniment au dé est un évènement qui n’a aucune chance de se réaliser et est bien négligeable. Il est cependant possible, au sens que rien n’empêche qu’il puisse se produire. ↩︎
On dit aussi certain.↩︎
“Symétrie” est le terme usité, au lieu de “commutativité”, car une opération commutative est plutôt une opération interne. La symétrie signifie la possibilité de permuter l’ordre des arguments d’une fonction sans modifier son résultat.↩︎
Géométriquement, elle exprime que le chemin le plus court entre deux points est la ligne droite : passer par un point intermédiaire est plus long.↩︎
Bizarrement, cette démonstration est plus fréquente que celle géométrique, qui est pourtant de loin plus naturelle, au sens de fondée sur une intuition géométrique essentielle.↩︎
Unitaire ou normé : de taille un.↩︎
Régression : réduction d’une variable à une autre.↩︎
Au sens étymologique : composé de parties interconnectées.↩︎
La notation pour la fonction de probabilité est surchargée. Précisément, on attribue à la fonction \(\proba{}\) un type dépendant : \(\forall n \in \mathbb{N}, \mathcal{S}_n \rightarrow [0,1],\) où \(\mathcal{S}_n\) est l’ensemble des séquences de taille \(n.\) Le paramètre \(n\) est laissé implicite : on abège \(\proba{}\ n\ S_n\) en \(\proba{}\ S_n\), où la valeur de \(n\) est inférée comme étant la taille de \(S_n\).↩︎
On dit qu’elles sont identiquement distribuées.↩︎