4  Exercices

\[ \newcommand{\Nat}{\mathbb{N}} \newcommand{\fctn}[3]{#1\ :\ #2 \rightarrow #3} \newcommand{\valE}{\mathtt{e}} \newcommand{\logNat}{\mathtt{ln}} \newcommand{\log}{\mathtt{log}} \newcommand{\Reel}{\mathbb{R}} \]

4.1 Résolution d’équations

4.1.1 Règles applicables pour la résolution d’équations linéaires (Seconde)

Avant de proposer les exercices, rappelons les règles fondamentales utilisées pour résoudre les équations linéaires¹. Ces règles sont fondées sur les propriétés algébriques des opérations sur les nombres et sont suffisantes pour résoudre les équations linéaires, d’une manière directe. Elles peuvent aussi être utilisées pour résoudre toute équation, mais requièrent alors une stratégie dédiée, comme celle utilisée pour résoudre des équations du second degré.

1. Distributivité : la distributivité permet de développer une expression de la forme \(a \cdot (b + c)\) en \(a \cdot b + a \cdot c,\) et inversement de factoriser \(a \cdot b + a \cdot c\) en \(a \cdot (b + c).\) Les opérations numériques, soit l’addition et la multiplication, étant commutatives², il est possible de commuter les termes des additions et des multiplications sans changer le résultat : autrement dit, l’égalité \[ a \cdot b + a \cdot c = a \cdot (b + c) \] a trente et une³ formes équivalentes, comme \[ a\cdot c + b \cdot a = a \cdot (b + c). \] Elles doivent être reconnues comme essentiellement la même égalité, du fait de la commutativité.

   Interprétation en termes d’aires : imaginez un rectangle de largeur \(a\) et de longueur \(b + c.\) Son aire est \(a \cdot (b + c).\) Si vous divisez ce rectangle en deux rectangles de largeurs \(b\) et \(c,\) les aires sont \(a \cdot b\) et \(a\cdot c.\) Ainsi, l’aire totale est \(a \cdot b + a \cdot c,\) ce qui justifie la loi de distributivité \[ a \cdot (b + c) = a \cdot b + a \cdot c. \]

Figure 4.1: Distributivité : une loi naturelle pour les aires

2. Simplifications fondamentales

   • Pour l’addition : si \(a + b = c,\) alors \(a = c - b.\)

     Justification : ajoutez \(-b\) aux deux membres : \((a + b) + (-b) = c + (-b).\) Par l’associativité de l’addition, \(a + (b + (-b)) = c - b.\) Comme \(b + (-b) = 0,\) on obtient \(a = c - b.\)
     

   • Pour la multiplication : si \(a \cdot b = c\) et \(b \neq 0,\) alors \(a = \dfrac{c}{b}.\)

     Justification : multipliez les deux membres par \(\dfrac{1}{b}\) : \((a \cdot b) \cdot \dfrac{1}{b} = c \cdot \dfrac{1}{b}.\) Par l’associativité de la multiplication, \(a \cdot (b \cdot \dfrac{1}{b}) = \dfrac{c}{b}.\) Comme \(b \cdot \dfrac{1}{b} = 1,\) on obtient \(a = \dfrac{c}{b}.\)

4.1.2 Exercices de résolution d’équations

Voici quatre exercices mettant en pratique ces règles. Chaque exercice mélange des nombres et des paramètres littéraux, et demande des simplifications. Les solutions détaillent les règles appliquées à chaque étape.

Exercice 4.1 (Résolution d’une équation linéaire algébriquement) Résoudre les quatre équations suivantes.

1. \(3 \cdot (x + 2) - 2 \cdot x = 4 - (x - 1).\)
2. \(a \cdot (x - b) = c \cdot (x + d),\) où \(a,\) \(b,\) \(c,\) \(d\) sont des paramètres avec \(a \neq c.\)
3. \(\dfrac{2\cdot x - 1}{3} + \dfrac{x + 2}{2} = 4.\)
4. \(m \cdot x + n = p \cdot (x - q) + r,\) où \(m,\) \(n,\) \(p,\) \(q,\) \(r\) sont des paramètres avec \(m \neq p.\)

Solution de l’équation 1

1. Appliquer la distributivité pour développer les expressions : \[ 3 \cdot x + 6 - 2 \cdot x = 4 - x + 1. \]
2. Simplifier chaque membre : \[ (3 \cdot x - 2 \cdot x) + 6 = (4 + 1) - x \quad \Rightarrow \quad x + 6 = 5 - x. \]
3. Isoler les termes en \(x\) en ajoutant \(x\) aux deux membres (règle de simplification pour l’addition) : \[ x + 6 + x = 5 - x + x \quad \Rightarrow \quad 2 \cdot x + 6 = 5. \]
4. Isoler le terme en \(x\) en soustrayant 6 des deux membres : \[ 2 \cdot x + 6 - 6 = 5 - 6 \quad \Rightarrow \quad 2 \cdot x = -1. \]
5. Diviser par \(2\) (règle de simplification pour la multiplication) : \[ x = \dfrac{-1}{2}. \]

Solution finale : \(x = -\dfrac{1}{2}\)

Solution de l’équation 2

1. Appliquer la distributivité pour développer : \[ a\cdot x - a\cdot b = c\cdot x + c\cdot d. \]
2. Isoler les termes en \(x\) en soustrayant \(cx\) des deux membres : \[ a\cdot x - a\cdot b - c\cdot x = c\cdot x + c\cdot d - c\cdot x \quad \Rightarrow \quad (a - c)\cdot x - a \cdot b = c \cdot d. \]
3. Isoler le terme en \(x\) en ajoutant \(ab\) aux deux membres : \[ (a - c)\cdot x - a \cdot b + a \cdot b = c \cdot d + a \cdot b \quad \Rightarrow \quad (a - c)\cdot x = a\cdot b + c\cdot d. \]
4. Diviser par \(a - c\) (puisque \(a \neq c\)) : \[ x = \dfrac{a\cdot b + c\cdot d}{a - c}. \]

Solution finale : \(x = \dfrac{a\cdot b + c\cdot d}{a - c}\)

Solution de l’équation 3

1. Mettre au même dénominateur (6) pour éliminer les fractions : \[ \dfrac{2\cdot (2\cdot x - 1) + 3\cdot (x + 2)}{6} = 4 \]
2. Appliquer la distributivité au numérateur : \[ \dfrac{4\cdot x - 2 + 3\cdot x + 6}{6} = 4 \quad \Rightarrow \quad \dfrac{7\cdot x + 4}{6} = 4. \]
3. Multiplier les deux membres par 6 pour éliminer le dénominateur : \[ 7\cdot x + 4 = 24. \]
4. Isoler \(x\) en soustrayant 4 des deux membres : \[ 7\cdot x + 4 - 4 = 24 - 4 \quad \Rightarrow \quad 7 \cdot x = 20. \]
5. Diviser par 7 : \[ x = \dfrac{20}{7}. \]

Solution finale : \(x = \dfrac{20}{7}\)

Solution de l’équation 4

1. Appliquer la distributivité au membre de droite : \[ m\cdot x + n = p\cdot x - p\cdot q + r. \]
2. Isoler les termes en \(x\) en soustrayant \(px\) des deux membres : \[ m\cdot x + n - p\cdot x = p\cdot x - p\cdot q + r - p\cdot x \quad \Rightarrow \quad (m - p)\cdot x + n = -p\cdot q + r. \]
3. Isoler le terme en \(x\) en soustrayant \(n\) des deux membres : \[ (m - p)\cdot x + n - n = -p\cdot q + r - n \quad \Rightarrow \quad (m - p)\cdot x = r - n - p\cdot q. \]
4. Diviser par \(m - p\) (puisque \(m \neq p\)) : \[ x = \dfrac{r - n - p\cdot q}{m - p}. \]

Solution finale : \(x = \dfrac{r - n - p\cdot q}{m - p}\)

Conclusion : Ces exercices illustrent l’application systématique de la distributivité et des règles de simplification pour résoudre des équations linéaires. La maîtrise de ces règles est essentielle pour aborder des problèmes plus complexes.

4.2 Suites

4.2.1 Sur les variations d’une suite

Soit \((u_n)\) une suite.

Propriété à étudier : la comparaison entre \(u_n\) et \(u_{n+1}\) pour tout entier naturel \(n.\)

• Si \(\forall n \in \Nat{}, u_n \leq u_{n+1},\) alors la suite est croissante,
• Si \(\forall n \in \Nat{}, u_n \geq u_{n+1},\) alors la suite est décroissante.
• Si la suite vérifie l’une des propriétés précédentes, elle est monotone.

Voici des méthodes génériques pour déterminer les variations d’une suite \((u_n).\)

Méthode algébrique – Etudier le signe de la différence \(u_{n+1} - u_n\) ou si \(u_n\) est toujours strictement positive⁴, le rapport \(\dfrac{u_{n+1}}{u_n}\) relativement à \(1.\)

• Différence – Soit la suite \((u_n)\) définie par \(u_n = n^2 + 1.\) On calcule :
  \[ u_{n+1} - u_n = (n+1)^2 + 1 - (n^2 + 1) = 2\cdot n + 1 \]
  Comme \(2\cdot n + 1 > 0\) pour tout \(n \in \mathbb{N},\) la suite est strictement croissante.
• Rapport – Soit \((u_n)\) une suite à termes positifs définie par \(u_n = \dfrac{2^n}{n!}\) pour \(n \geq 1.\) On calcule le rapport :
  \[ \dfrac{u_{n+1}}{u_n} = \dfrac{2^{n+1}}{(n+1)!} \cdot \dfrac{n!}{2^n} = \dfrac{2}{n+1} \]
  Pour \(n \geq 1,\) on a \(\dfrac{2}{n+1} \leq 1,\) donc la suite est décroissante à partir du rang \(1.\)

Utilisation d’un encadrement – Dans certains cas, on peut déduire la monotonie en exprimant la différence \(u_{n+1} - u_n\) comme une expression dépendant de \(u_n,\) dont le signe est garanti si \((u_n)\) est encadrée.

• Soit \((u_n)\) la suite définie par \(u_0 = 2\) et \(u_{n+1} = \dfrac{u_n}{2} + \dfrac{1}{u_n}.\) On observe que \(u_{n+1} - u_n = \dfrac{1}{u_n} - \dfrac{u_n}{2}.\) Or si \(x\) est un réel strictement positif, \(\dfrac{1}{x} - \dfrac{x}{2} \leq 0\) est équivalent à \(\sqrt{2} \leq x.\) On montre alors par récurrence que pour tout \(n \geq 0,\) \(u_n \geq \sqrt{2}.\) On conclut que la suite est décroissante, puisque le signe de \(u_{n+1} - u_n\) est négatif.

Utilisation d’une fonction auxiliaire – Lorsque la suite est définie explicitement par \(u_n = f(n),\) où \(f\) est une fonction dérivable sur un intervalle \(I\) contenant les entiers naturels, on étudie les variations de \(f\) sur \(I.\)

• Soit \((u_n)\) la suite définie par \(u_n = \dfrac{n}{n^2 + 1}.\) Considérons la fonction \(f\) définie par \(f(x) = \dfrac{x}{x^2 + 1}\) pour \(x \geq 0.\) Sa dérivée vaut :
  \[ f'(x) = \dfrac{(x^2 + 1) - x \cdot 2x}{(x^2 + 1)^2} = \dfrac{1 - x^2}{(x^2 + 1)^2} \]
  Ainsi, \(f'(x) \geq 0\) pour \(x \in [0, 1]\) et \(f'(x) \leq 0\) pour \(x \geq 1.\) La suite \((u_n)\) est donc croissante pour \(n \leq 1\) et décroissante pour \(n \geq 1.\)

Démonstration par récurrence – Cette méthode est particulièrement utile lorsque les techniques algébriques directes sont difficiles à mettre en œuvre et lorsque la suite est définie par une relation de récurrence.

• Soit \((u_n)\) la suite définie par \(u_0 = 1\) et \(u_{n+1} = \sqrt{u_n + 2}.\) Montrons par récurrence que cette suite est croissante.
  • Initialisation : \(u_0 = 1,\) \(u_1 = \sqrt{3} \approx 1.732 > 1,\) donc \(u_1 \geq u_0.\)
    
  • Hérédité : supposons \(u_{n+1} \geq u_n\) pour un certain rang \(n.\) Alors :
    \[ u_{n+2} = \sqrt{u_{n+1} + 2} \geq \sqrt{u_n + 2} = u_{n+1} \] car la fonction \(x \mapsto \sqrt{x + 2}\) est croissante.
    
  • Conclusion : en appliquant le principe de récurrence, on conclut que \(\forall n \in \Nat{}, u_{n+1} \geq u_n\) et que la suite \((u_n)\) est croissante.

Préservation de l’ordre – Généralisation de l’argument précédent – Soit \((u_n)\) la suite définie par \(u_0 = c\) et \(u_{n+1} = f(u_n)\) où la fonction \(\fctn{f}{I}{I}\) est une fonction croissante sur l’intervalle \(I\) et \(c\) appartient à \(I.\) La suite \((u_n)\) est alors monotone.

• En effet, la croissance de la fonction \(f\) signifie qu’elle préserve l’ordre : \[ \forall x, y \in I, x \leq y \Rightarrow f(x) \leq f(y). \] Ainsi si \(u_0 \leq u_1,\) on obtient \(f(u_0) \leq f(u_1),\) soit \(u_1 \leq u_2,\) et ainsi de suite par récurrence, et symétriquement si \(u_0 \geq u_1.\)

• Exemple précédent : \(u_{n+1} = \sqrt{u_n + 2}\) avec \(I = [1, 2].\) Sur l’intervalle \(I = [2, +\infty[,\) la suite devient décroissante.
  

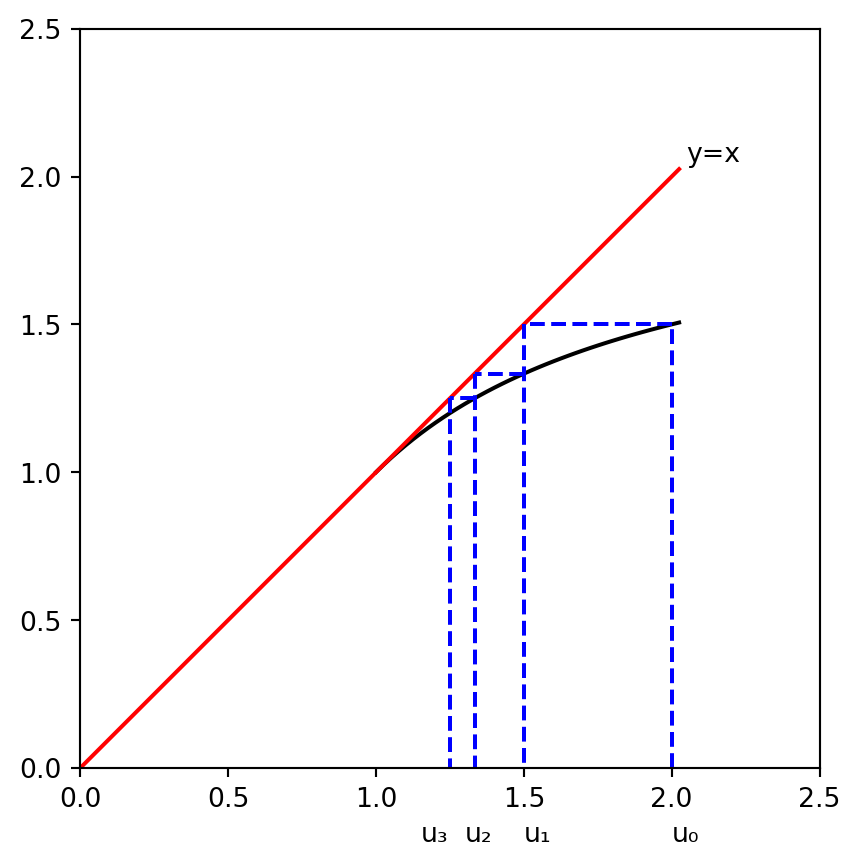
• Autre exemple : \(u_{n+1} = 2 - 1/u_n,\) avec \(I = [1, 2].\) Pour \(c \in I,\) on a \(c \geq 2 - 1/c,\) car \(c^2 - 2 \cdot c + 1 = (c - 1)^2\) est positif. La suite est donc décroissante. Voir la figure Figure 4.2 pour la construction graphique des termes de la suite qui se réalise ainsi, pour toute suite \((u_n)\) définie par la relation de récurrence \(u_{n+1} = f(u_n)\) :

  1. partant du point \((u_0, 0),\) on monte verticalement jusqu’au point \((u_0, f(u_0)),\) soit \((u_0, u_1),\) situé sur la courbe,
  2. on reporte horizontalement le point \((u_0, u_1)\) sur la première bissectrice (droite d’équation \(y = x\)), pour obtenir \((u_1, u_1),\)
  3. on projette ce point sur l’axe des abscisses pour obtenir le point \((u_1, 0),\)
  4. on continue comme à l’étape 1 à partir du point \((u_1, 0).\)

import math 
import numpy as np
import matplotlib.pyplot as plt

def premiereBissectrice(x) :
    return x

def f(x) :
    return 2 - 1/x

def premiereMontee(u0, u1) :
    plt.plot([u0, u0], [0, u1], 'b--')

def marche(u0, u1, u2) :
    plt.plot([u0, u1], [u1, u1], 'b--')
    plt.plot([u1, u1], [u1, 0], 'b--')


t1 = np.arange(1.0, 2.05, 0.025)
plt.plot(t1, list(map(f, t1)), 'k')
t1 = np.arange(0.0, 2.05, 0.025)
plt.plot(t1, list(map(premiereBissectrice, t1)), 'r')

x0 = 2.0
x1 = f(x0) 
premiereMontee(x0, x1)
x2 = f(x1)
marche(x0, x1, x2)
x3 = f(x2)
marche(x1, x2, x3) 
x4 = f(x3)
marche(x2, x3, x4) 

plt.text(2.0, -0.25, 'u₀')
plt.text(1.5, -0.25, 'u₁')
plt.text(1.30, -0.25, 'u₂')
plt.text(1.15, -0.25, 'u₃')
plt.text(2.05, 2.05, 'y=x')

plt.xlim(0, 2.5)
plt.ylim(0, 2.5)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')

plt.show()

Figure 4.2: Suite récurrente décroissante – Construction en escalier des termes

Expansion ou contraction – Une fonction \(f\) est dite expansive si pour tout \(x, f(x) \geq x,\) et contractante si pour tout \(x, f(x) \leq x.\) Soit \((u_n)\) une suite vérifiant la relation de récurrence \(u_{n+1} = f(u_n)\) où la fonction \(\fctn{f}{I}{I}\) est une fonction définie sur l’intervalle \(I.\) Propriété : si \(f\) est expansive, alors la suite \((u_n)\) est croissante ; si \(f\) est contractante, alors la suite \((u_n)\) est décroissante.

• C’est immédiat par définition de la suite \((u_n)\) à partir de \(f.\) C’est donc la position du graphe de \(f\) relativement à la première bissectrice⁵ qui importe.

4.2.2 Exercices sur les suites

Exercice 4.2 (Variations de suites) Étudier le sens de variation des suites suivantes.

1. \(\Big(u_n := \dfrac{3\cdot n − 5}{4\cdot n + 5}\Big).\)
2. Généralisation : \(\Big(u_n := \dfrac{\alpha \cdot n + a}{\beta \cdot n + b}\Big),\) où \(\alpha\) et \(\beta\) sont des réels non nuls, \(a\) est un réel et \(b\) un réel tel que \(-b/\beta \notin \Nat{}.\)
3. \(\begin{cases} u_0 = 1, \\ u_{n+1} = 2 \cdot u_{n} - 3. \\ \end{cases}\)

Solution 1

Toute fraction rationnelle peut se décomposer en une forme pratique⁶ : \[ \begin{array}{rcl} \dfrac{3\cdot n − 5}{4\cdot n + 5} & =& \dfrac{3/4 \cdot (4\cdot n + 5) − 15/4 - 5}{4\cdot n + 5} \\ &=& \dfrac{3}{4} - \dfrac{35/4}{4\cdot n + 5} \end{array} \]

Ainsi la limite \(3/4\) apparaît immédiatement et la croissance de la suite se déduit de la décroissance de la fonction \(\Big(x \mapsto \dfrac{1}{4\cdot x + 5}\Big)\) sur l’intervalle \(]-5/4, +\infty[\) qui contient \(\Nat{}.\)

Solution 2

Soient \(\alpha\) et \(\beta\) des réels non nuls, \(a\) un réel et \(b\) un réel tel que \(-b/\beta \notin \Nat{}.\) Quitte à prendre l’opposé du numérateur et du dénominateur, on peut supposer \(\beta > 0.\) Simplifions :

\[ \begin{align*} u_n &= \dfrac{\alpha \cdot n + a}{\beta \cdot n + b} \\ &= \dfrac{(\beta \cdot n + b) \cdot (\alpha / \beta) + a - (b \cdot \alpha / \beta)}{\beta \cdot n + b}\\ &= (\alpha / \beta) + \dfrac{a - (b \cdot \alpha / \beta)}{\beta \cdot n + b}\\ \end{align*} \] Comme \(\beta\) est supposé strictement positif, la fonction \((x \mapsto \beta \cdot x + b)\) est strictement croissante. Par inversion, la fonction \((x \mapsto 1/(\beta \cdot x + b))\) est décroissante, à gauche de \(-b/\beta\) et à droite de \(-b/\beta\), et toute valeur à gauche de \(-b/\beta\) est inférieure à toute valeur à droite de \(-b/\beta\)⁷. Il s’ensuit que la suite \((1/(\beta \cdot n + b))\) est décroissante pour les entiers naturels inférieurs à \(-b/\beta\), décroissante pour les entiers naturels supérieurs à \(-b/\beta\), et croissante entre \(p\) et \(p+1\), si la partie entière \(p\) de \(-b/\beta\) est un entier naturel. Le sens de variation de \((u_n)\) se déduit, suivant le signe du facteur \(a - (b \cdot \alpha / \beta) :\) s’il est positif, rien n’est modifié, s’il est négatif, les variations sont inversées, et s’il est nul, la suite est constante.

Solution 3

La suite \((u_n)\) est une suite arithmético-géométrique. On remarque que la différence \(u_{n+1} - u_n\) est égale à \(u_n - 3.\) Ainsi si la suite \((u_n)\) est majorée par \(3,\) la suite est décroissante. Montrons par récurrence que la suite \((u_n)\) est effectivement majorée par \(3.\)

Initialisation : \(n = 0.\) On a bien \(u_0 \leq 3.\)

Hérédité : soit \(n \geq 0\) un entier naturel et supposons \(u_n \leq 3.\) Ainsi \(u_n - 3 \leq 0\), donc \(u_{n+1} - u_n \leq 0,\) ce qui donne \(u_{n+1} \leq u_n\), ce qui donne par transitivité \(u_{n+1} \leq 3\).

Conclusion : en appliquant le principe de récurrence, on déduit que pour tout entier naturel \(n, u_n \leq 3\), et ainsi \(u_{n+1} \leq u_n.\)

C’est une méthode tout à fait générale pour montrer la monotonie d’une suite arithmético-géométrique : voir l’Exercice 4.4.

4.3 Suites arithmétiques et géométriques

Exercice 4.3 (Suites géométriques - Les bases) Soit \((v_n)\) une suite géométrique de premier terme \(c\) et de raison \(q\), où \(c\) est un réel non nul et \(q\) est un réel différent de \(0\) et de \(1.\)

1. Rappeler la relation de récurrence de la suite.
2. Exprimer \(v_n\) en fonction de \(n\) (expression explicite de la suite) et démontrer par récurrence la validité de l’expression.
3. Donner le sens de variation de la suite. Justifier votre réponse.
4. Pour tout entier naturel non nul \(p\), calculer la somme \(S_p\) des termes d’indice impair entre \(3\) et \(2\cdot p +1 :\) \[ S_p = v_3 + v_5 + v_7 + \cdots + v_{2 \cdot p +1}. \]

1 et 2. De la relation de récurrence à l’expression explicite

La relation de récurrence pour une suite géométrique est \(v_{n+1} = q \cdot v_n.\) L’expression explicite s’obtient par itération : \(v_0 = c, v_1 = q \cdot v_0 = q \cdot c, v_2 = q \cdot v_1 = q^2 \cdot c, v_3 = q \cdot v_2 = q^3 \cdot c, \ldots, v_n = q^n \cdot c.\) Montrons-le par récurrence.

Initialisation : \(n = 0.\) \(v_0 = c = q^0 \cdot c\) puisque \(q^0 = 1.\)

Hérédité : soit \(n \geq 0\) un entier naturel et supposons \(v_n = q^n \cdot c.\) Montrons \(v_{n+1} = q^{n+1} \cdot c.\) Or \(v_{n+1} = q \cdot v_n = q \cdot q^{n} \cdot c = q^{n+1} \cdot c\).

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n, v_n = q^n \cdot c.\)

3. Sens de variation

Soit \(n\) un entier naturel et comparons \(v_{n+1}\) et \(v_n\), par exemple en étudiant le signe de \(v_{n+1} - v_n.\)

\[ v_{n+1} - v_n = q^{n+1} \cdot c - q^{n} \cdot c = q^{n} \cdot c \cdot (q - 1). \]

Distinguons les différents cas possibles.

• \(q > 0\) : la suite est monotone car le signe est constant, et la monotonie est stricte, car la différence n’est jamais nulle.
  • \(c > 0\)
    • \(q > 1\) : suite croissante
    • \(q < 1\) : suite décroissante
  • \(c < 0\)
    • \(q > 1\) : suite décroissante
    • \(q < 1\) : suite croissante
• \(q < 0\) : la suite est alternée, puisque la différence est tantôt positive, tantôt négative.

4. Somme des termes impairs

Quand on passe du terme d’indice impair \(v_{2\cdot n +1}\) au suivant \(v_{2\cdot (n + 1) +1},\) le coefficient multiplicatif est désormais \(q^2 : v_{2\cdot n +3} = q^2 \cdot v_{2\cdot n +1}\). Autrement dit, la suite formée des termes d’indice impair est une suite géométrique de raison \(q^2.\) Calculons la somme \(S^p,\) étant donné un entier naturel \(p\) non nul.

\[ \begin{align*} S_p &= \sum_{n = 1}^{p} v_{2\cdot n +1} \\ S_p &= v_3 + v_5 + \ldots + v_{2\cdot p - 1} + v_{2\cdot p +1} \\ q^2 \cdot S_p &= v_5 + v_7 + \ldots + v_{2\cdot p +1} + v_{2\cdot p +3}\\ S_p \cdot (1 - q^2) &= v_3 - v_{2\cdot p +3} \\ S_p &= \dfrac{q^3 \cdot (1 - q^{2\cdot p}) \cdot c}{1 - q^2}. \\ \end{align*} \]

Exercice 4.4 (Suites arithmetico-géométriques - Les bases) Soit \((u_n)\) la suite définie par \(u_0 = c\) et pour tout \(n\in \Nat{}, u_{n+1} = a \cdot u_n + b,\) où \(c\) est un réel, \(a\) un réel positif différent de \(0\) et de \(1\) et \(b\) un réel différent de \(0.\)

1. Calculer la valeur \(l\) de la suite constante \((k_n)\) vérifiant la relation de récurrence \(k_{n+1} = a \cdot k_n + b.\)
2. Montrer par récurrence que la suite \((u_n)\) est soit minorée par \(l\), soit majorée par \(l:\) soit \(\forall n \in \Nat{}, u_n \geq l,\) soit \(\forall n \in \Nat{}, u_n \leq l.\)
3. En déduire que la suite est monotone.
4. Déterminer la formule explicite \(f\) de la suite \((u_n) : \forall n \in \Nat{}, u_n = f(n).\) Indication : utiliser le fait que \((u_n)\) et \((k_n)\) vérifient la même relation de récurrence.
5. Montrer par récurrence que pour tout entier naturel \(n, u_n\) est égal à \(f(n).\)

1,2 et 3. Encadrement de la suite et monotonie

\(l\) vérifie l’équation \(l = a \cdot l + b,\) soit \(l = \dfrac{b}{1 - a}.\) Envisageons deux cas, suivant la valeur initiale de la suite.

• \(c \geq l.\) Montrons par récurrence que \(\forall n \in \Nat{}, u_n \geq l.\)
  • Initialisation. \(n = 0 :\) c’est notre hypothèse pour ce cas.
  • Hérédité. Soit \(n \in \Nat{}\). Supposons \(u_n \geq l\). Montrons \(u_{n+1} \geq l.\) Or comme la fonction \((x \mapsto a \cdot x + b)\) est croissante, de l’hypothèse de récurrence, on déduit \(a \cdot u_n + b \geq a \cdot l + b,\) autrement dit \(u_{n+1} \geq l.\)
• \(c < l.\) Montrons par récurrence que \(\forall n \in \Nat{}, u_n \leq l.\)⁸ On reproduit exactement le même raisonnement.

Pour déterminer la monotonie, considérons la différence \(u_{n+1} - u_n\), pour \(n\) entier naturel, et déterminons son signe. \[ u_{n+1} - u_n = (a - 1) \cdot u_n + b. \] Or \((a - 1) \cdot u_n + b \geq 0\) est équivalent, après multiplication par \(1/(a-1)\), à \(u_n \geq l\) si \(a > 1\) et à \(u_n \leq l\) si \(a < 1\), et de même pour \(\leq\). Ainsi la suite est croissance lorsque

• la suite est minorée par \(l\) et le coefficient \(a\) est strictement supérieur à \(1,\)
• la suite est majorée par \(l\) et le coefficient \(a\) est strictement inférieur à \(1,\)

et décroissante lorsque

• la suite est majorée par \(l\) et le coefficient \(a\) est strictement supérieur à \(1,\)
• la suite est minorée par \(l\) et le coefficient \(a\) est strictement inférieur à \(1.\)

4 et 5. Formule explicite

\((u_n)\) et \((k_n)\) (la suite constante \((l)\)) vérifient la même relation de récurrence : \[ \begin{align*} u_{n+1} &= a \cdot u_n + b, \\ k_{n+1} &= a \cdot k_n + b. \\ \end{align*} \] Par soustraction, on obtient \(u_{n+1} - k_{n+1} = a \cdot (u_n - k_n)\). Autrement dit, la suite \((u_n - k_n)\) est une suite géométrique de raison \(a\), dont la formule explicite est \(u_n - k_n = a^n \cdot (u_0 - k_0),\) soit \[ u_n = l + a^n \cdot (c - l). \]

On retrouve ainsi la caractérisation précédente de la monotonie.

Montrons par récurrence la validité de cette formule explicite.

• Initialisation : \(n = 0.\) \(u_0 = c\) et \(l + a^0 \cdot (c - l) = l + 1 \cdot (c - l) = c :\) l’égalité est vérifiée.
• Hérédité. Soit \(n\in\Nat{}\), et supposons \(u_n = l + a^n \cdot (c - l).\) On a : \[ \begin{align*} u_{n+1} &= a \cdot u_n + b \\ &= a \cdot (l + a^n \cdot (c - l)) + b \quad \textrm{(hypothèse de récurrence)} \\ &= a \cdot l + b + a^{n+1} \cdot (c - l) \\ &= l + a^{n+1} \cdot (c - l). \end{align*} \]

4.4 Récurrence

L’exercice suivant est extrait du Tome 1 (arithmétique, algèbre, analyse) de Combes et Bargues (1977).

Exercice 4.5 (Démontrer par récurrence) Démontrer par récurrence les propriétés suivantes.

1. Pour tout entier naturel \(n,\) \(3^{2\cdot n +2} - 2^{n+1}\) est un multiple de \(7.\)
2. Pour tout entier naturel \(n,\) \(10^{6\cdot n + 2} + 10^{3\cdot n + 1} + 1\) est un multiple de \(111.\)
3. Pour tout entier naturel non nul \(n,\) \[ \dfrac{1}{1\cdot 2 \cdot 3} + \dfrac{1}{2\cdot 3 \cdot 4} + \ldots + \dfrac{1}{n\cdot (n+1) \cdot (n+2)} = \dfrac{n\cdot (n+3)}{4\cdot (n+1)\cdot(n+2)}. \]
4. Pour tout entier naturel \(n\) strictement supérieur à \(1,\) \[ \dfrac{2^{2\cdot n - 1}}{n} < \binom{2\cdot n}{n} < 2^{2\cdot n - 1}, \] où \(\dbinom{p}{n} = \dfrac{p!}{n! \cdot (p -n)!}\) est le coefficient binomial “\(n\) parmi \(p.\)”
5. Étant donné un entier naturel \(p,\) pour tout entier naturel non nul \(n,\) \[ \sum_{i = 1}^n \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{n!}{(n+p)!}\Big). \]

Solution 1 – Multiple de 7 ?

Initialisation : \(n = 0.\) \(3^{2} - 2^{1},\) soit \(7,\) est bien un multiple de \(7.\)

Hérédité : soit \(n \geq 0\) un entier naturel et supposons que \(3^{2\cdot n +2} - 2^{n+1}\) soit un multiple de \(7.\) Montrons que \(3^{2\cdot n + 4} - 2^{n+2}\) est un multiple de \(7.\) Or \[ \begin{array}{rcl} 3^{2\cdot n + 4} - 2^{n+2} & = & 3^2 \cdot 3^{2\cdot n + 2} - 2 \cdot 2^{n+1} \\ & = & (7 + 2) \cdot 3^{2\cdot n + 2} - 2 \cdot 2^{n+1} \\ & = & 7 \cdot 3^{2\cdot n + 2} + 2 \cdot (3^{2\cdot n + 2} - 2^{n+1}). \\ \end{array} \] Par l’hypothèse de récurrence, \(3^{2\cdot n + 2} -2^{n+1}\) est un multiple de \(7.\) Les multiples de \(7\) étant stables⁹ par la multiplication par un scalaire (par un réel, ici \(2\)) et l’addition, on déduit que \(3^{2\cdot n + 4} - 2^{n+2}\) est un multiple de \(7.\)

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n, 3^{2\cdot n +2} - 2^{n+1}\) est un multiple de \(7.\)

Solution 2 – Multiple de 111 ?

Initialisation : \(n = 0.\) \(10^{2} + 10^{1} + 1,\) soit \(111,\) est bien un multiple de \(111.\)

Hérédité : soit \(n \geq 0\) un entier naturel et supposons que \(10^{6\cdot n + 2} + 10^{3\cdot n + 1} + 1\) soit un multiple de \(111.\) Montrons que \(10^{6\cdot (n+1) + 2} + 10^{3\cdot (n+1) + 1} + 1\) est un multiple de \(111.\) Or, en remarquant¹⁰ que \[ \begin{array}{rcl} 10^3 &=& 9 \cdot 111 + 1,\\ 10^6 &=& 9 \cdot 111111 + 1 \\ &=& 9 \cdot (111 \cdot 10^3 + 111) +1 \\ &=& 9 \cdot 1001 \cdot 111 + 1 \\ &=& 9009 \cdot 111 + 1, \] on obtient \[ \begin{array}{rcl} 10^{6\cdot (n+1) + 2} + 10^{3\cdot (n+1) + 1} + 1 & = & 10^{6\cdot n + 8} + 10^{3\cdot n + 4} + 1 \\ & = & 10^6 \cdot 10^{6\cdot n + 2} + 10^3 \cdot 10^{3\cdot n + 1} + 1 \\ & = & (9009 \cdot 111 + 1) \cdot 10^{6\cdot n + 2} + (9 \cdot 111 + 1) \cdot 10^{3\cdot n + 1} + 1 \\ & = & k \cdot 111 + 10^{6\cdot n + 2} + 10^{3\cdot n + 1} + 1. \\ \end{array} \] Par l’hypothèse de récurrence, \(10^{6\cdot n + 2} + 10^{3\cdot n + 1} + 1\) est un multiple de \(111.\) Les multiples de \(111\) étant stables par addition, on déduit que \(10^{6\cdot (n+1) + 2} + 10^{3\cdot (n+1) + 1} + 1\) est un multiple de \(111.\)

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n, 10^{6\cdot n + 2} + 10^{3\cdot n + 1} + 1\) est un multiple de \(111.\)

Solution 3 – Somme de fractions

On considère la somme \[ \sum_{k = 1}^n \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \dfrac{1}{1\cdot 2 \cdot 3} + \dfrac{1}{2\cdot 3 \cdot 4} + \ldots + \dfrac{1}{n\cdot (n+1) \cdot (n+2)}. \]

Initialisation : \(n = 1.\) On a : \[ \sum_{k = 1}^1 \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \dfrac{1}{1\cdot (1+1) \cdot (1+2)} = \dfrac{1\cdot (1+3)}{4\cdot (1+1)\cdot(1+2)}, \] après simplification par \(4.\) L’égalité est bien vérifiée en \(n = 1.\)

Hérédité : soit \(n \geq 1\) et supposons \[ \sum_{k = 1}^n \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \dfrac{n\cdot (n+3)}{4\cdot (n+1)\cdot(n+2)}. \] Montrons \[ \sum_{k = 1}^{n+1} \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \dfrac{(n + 1)\cdot (n+4)}{4\cdot (n+2)\cdot(n+3)}. \] Or \[ \begin{align*} \sum_{k = 1}^{n+1} \dfrac{1}{k\cdot (k+1) \cdot (k+2)} &= \sum_{k = 1}^{n} \dfrac{1}{k\cdot (k+1) \cdot (k+2)} \\ &+ \dfrac{1}{(n+1)\cdot (n+2) \cdot (n+3)}\\ &= \dfrac{n\cdot (n+3)}{4\cdot (n+1)\cdot(n+2)} \quad \textrm{(hypothèse de récurrence)}\\ &+ \dfrac{1}{(n+1)\cdot (n+2) \cdot (n+3)} & \\ &= \dfrac{n\cdot (n+3)^2 + 4}{4 \cdot (n+1)\cdot (n+2) \cdot (n+3)}\\ &= \dfrac{(n + 1) \cdot (n^2 + 5 \cdot n + 4)}{4 \cdot (n+1)\cdot (n+2) \cdot (n+3)} \quad \textrm{(factorisations)}\\ &= \dfrac{(n + 1) \cdot (n + 1) \cdot (n + 4)}{4 \cdot (n+1)\cdot (n+2) \cdot (n+3)}\\ &= \dfrac{(n + 1)\cdot (n+4)}{4\cdot (n+2)\cdot(n+3)}. \end{align*} \]

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n \geq 1,\) \[ \sum_{k = 1}^n \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \dfrac{n\cdot (n+3)}{4\cdot (n+1)\cdot(n+2)}. \]

Solution 3 – Complément : déterminer la formule explicite.

Quand la formule explicite est donnée, la démarche est claire : démontrer la validité de la formule par récurrence. Mais comment trouver la formule explicite ? L’espace des possibilités est ici beaucoup plus vaste, et il convient de développer progressivement un répertoire de méthodes et de techniques de résolution. Pour la somme qui nous intéresse, nous pouvons appliquer une méthode générale adaptée aux fractions. En effet, nous devons sommer des fractions de la forme \(\dfrac{1}{A\cdot B \cdot C}.\) Une telle fraction devrait pouvoir s’obtenir comme une somme de fractions de la forme \(\dfrac{\alpha}{A} + \dfrac{\beta}{B} + \dfrac{\gamma}{C}\) puisque la réduction au même dénominateur donne le dénominateur attendu \(A\cdot B \cdot C :\) \[ \dfrac{\alpha}{A} + \dfrac{\beta}{B} + \dfrac{\gamma}{C} = \dfrac{\alpha\cdot B \cdot C + A\cdot \beta \cdot C + A\cdot B \cdot \gamma}{A\cdot B \cdot C}. \] Voyons s’il est possible de déterminer \(\alpha, \beta, \gamma\) vérifiant \[ \alpha\cdot B \cdot C + A\cdot \beta \cdot C + A\cdot B \cdot \gamma = 1. \]

C’est probable car \(A, B, C\) sont des polynômes affines si bien que l’équation précédente est une égalité entre un polynôme de degré deux et l’unité, ce qui donne trois équations linéaires pour trois inconnues. Construisons ce système pour le terme en \(n-1.\) \[ \begin{array}{cl} & \alpha\cdot n \cdot (n+1) + (n-1)\cdot \beta \cdot (n+1) + (n-1)\cdot n \cdot \gamma \\ = &(\alpha + \beta + \gamma)\cdot n^2 + (\alpha - \gamma) \cdot n + \alpha - \beta - \gamma \\ = & 0 \cdot n^2 + 0 \cdot n + 1.\\ \end{array} \] L’égalité des polynômes produit trois équations qu’on peut résoudre. Alternativement, l’égalité valant pour tout \(n,\) on peut l’instancier avec des \(n\) bien choisis, ceux annulant les trois polynômes affines : \(n = 0\) donne \(\beta = -1,\) \(n=1\) donne \(\alpha = 1/2\) et \(n=-1\) donne \(\gamma = 1/2.\) On vérifie alors que ce sont les solutions du système déduit précédemment de l’égalité polynomiale.

La somme à calculer se récrit ainsi : \[ \sum_{k = 1}^n \dfrac{1}{k\cdot (k+1) \cdot (k+2)} = \sum_{k = 1}^n \Big( \dfrac{1/2}{k} + \dfrac{(-1)}{k+1} + \dfrac{1/2}{k+2}\Big). \]

En développant la somme, on constate que les termes consécutifs se simplifient¹¹ : \[ \begin{align*} \sum_{k = 1}^n \Big( \dfrac{1/2}{k} + \dfrac{(-1)}{k+1} + \dfrac{1/2}{k+2}\Big) &= \dfrac{1/2}{1} + \dfrac{(-1)}{2} + \cancel{\dfrac{1/2}{3}} \\ &+\dfrac{1/2}{2} + \cancel{\dfrac{(-1)}{3}} + \cancel{\dfrac{1/2}{4}} \\ &+ \cancel{\dfrac{1/2}{3}} + \cancel{\dfrac{(-1)}{4}} + \cancel{\dfrac{1/2}{5}} \\ &+ \ldots + \ldots + \ldots \\ &+ \cancel{\dfrac{1/2}{n-2}} + \cancel{\dfrac{(-1)}{n-1}} + \cancel{\dfrac{1/2}{n}} \\ &+ \cancel{\dfrac{1/2}{n-1}} + \cancel{\dfrac{(-1)}{n}} + \dfrac{1/2}{n+1} \\ &+ \cancel{\dfrac{1/2}{n}} + \dfrac{(-1)}{n+1} + \dfrac{1/2}{n+2}, \\ \end{align*} \]

ce qui donne finalement la formule après l’élimination des termes et une réduction des fractions au même dénominateur, \[ \begin{align*} \sum_{k = 1}^n \Big( \dfrac{1/2}{k} + \dfrac{(-1)}{k+1} + \dfrac{1/2}{k+2}\Big) &= \dfrac{1/2}{1} + \dfrac{(-1)}{2} \\ &+ \dfrac{1/2}{2} + \dfrac{1/2}{n+1} \\ &+ \dfrac{(-1)}{n+1} + \dfrac{1/2}{n+2} \\ &= \dfrac{1}{4} + \dfrac{- n - 2 + n + 1}{2 \cdot (n+1) \cdot (n+2)} \\ &= \dfrac{(n + 1)\cdot(n+2) -2}{4 \cdot (n+1) \cdot (n+2)} \\ &= \dfrac{n^2 + 3 \cdot n + 2 -2}{4 \cdot (n+1) \cdot (n+2)} \\ &= \dfrac{n\cdot (n + 3)}{4 \cdot (n+1) \cdot (n+2)}. \\ \end{align*} \]

Solution 4 - Encadrement de coefficients binomiaux

Initialisation : \(n = 2.\) On a \(\dfrac{2^{2\cdot 2 - 1}}{2} = 4, \binom{2\cdot 2}{2} = 6, 2^{2\cdot 2 - 1} = 8\) et $4 < 6 < 8. La propriété est vérifiée en \(n = 0\).

Hérédité : soit \(n \geq 2\) un entier naturel et supposons \[ \dfrac{2^{2\cdot n - 1}}{n} < \binom{2\cdot n}{n} < 2^{2\cdot n - 1}. \] Montrons \[ \dfrac{2^{2\cdot n + 1}}{n + 1} < \binom{2\cdot n + 2}{n + 1} < 2^{2\cdot n + 1}. \] Calculons : \[ \begin{align*} \binom{2\cdot n + 2}{n + 1} &= \dfrac{(2\cdot n + 2)!}{(n+1)! \cdot (n + 1)!} \\ &= \binom{2\cdot n}{n} \cdot \dfrac{(2\cdot n + 2)\cdot(2\cdot n + 1) }{(n+1) \cdot (n + 1)}\\ &= \binom{2\cdot n}{n} \cdot 4 \cdot \dfrac{(n + 1)\cdot(n + 1/2) }{(n+1) \cdot (n + 1)}\\ &= \binom{2\cdot n}{n} \cdot 4 \cdot \dfrac{n + 1/2 }{n + 1}.\\ \end{align*} \] En utilisant l’hypothèse de récurrence, on déduit la minoration suivante \[ \begin{align*} \binom{2\cdot n + 2}{n + 1} &> \dfrac{2^{2\cdot n - 1}}{n} \cdot 4 \cdot \dfrac{n + 1/2}{n + 1},\\ &> \dfrac{2^{2\cdot n + 1}}{n+1} \cdot \dfrac{n + 1/2}{n}\\ &> \dfrac{2^{2\cdot n + 1}}{n+1}\\ \end{align*} \] et la majoration suivante \[ \begin{align*} \binom{2\cdot n + 2}{n + 1} &< 2^{2\cdot n - 1} \cdot 4 \cdot \dfrac{n + 1/2 }{n + 1}\\ &< 2^{2\cdot n + 1} \cdot \dfrac{n + 1/2 }{n + 1}\\ &< 2^{2\cdot n + 1}.\\ \end{align*} \]

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n \geq 2,\) \[ \dfrac{2^{2\cdot n - 1}}{n} < \binom{2\cdot n}{n} < 2^{2\cdot n - 1}. \]

Solution 5 - Une somme de produits

Soit \(p\) un entier naturel. \(p\) pour tout entier naturel non nul \(n,\) \[ \sum_{i = 1}^n \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{n!}{(n+p)!}\Big). \]

Initialisation : \(n = 1.\) On a \[ \sum_{i = 1}^1 \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{\prod_{j = 0}^{p} (1 + j)} = \dfrac{1}{(p+1)!} \] et \[ \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{1!}{(1+p)!}\big) = \dfrac{1}{p} \cdot \Big(\dfrac{(p+1)}{(p+1)!} - \dfrac{1}{(1+p)!}\big) = \dfrac{1}{p} \cdot \dfrac{p}{(p+1)!} = \dfrac{1}{(p+1)!}, \] ce qui démontre l’égalité en \(n=0.\)

Hérédité : soit \(n \geq 1\) un entier naturel et supposons \[ \sum_{i = 1}^n \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{n!}{(n+p)!}\Big). \] Montrons \[ \sum_{i = 1}^{n+1} \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{(n+1)!}{(n+1+ p)!}\Big). \]

Or en décomposant la somme, en appliquant l’hypothèse de récurrence et en faisant apparaître des fractions de factorielles à la place des produits, on a : \[ \begin{align*} \sum_{i = 1}^{n+1} \dfrac{1}{\prod_{j = 0}^{p} (i + j)} &= \sum_{i = 1}^{n} \dfrac{1}{\prod_{j = 0}^{p} (i + j)} + \dfrac{1}{\prod_{j = 0}^{p} (n + 1 + j)} \\ &= \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{n!}{(n+p)!}\Big) + \dfrac{n!}{(n + 1 + p)!} \\ &=\dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{(n + p + 1) \cdot n!}{(n+p+1)!} + \dfrac{p\cdot n!}{(n + 1 + p)!}\Big) \\ &=\dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{(n + 1) \cdot n!}{(n+p+1)!} \Big) \\ &=\dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{(n + 1)!}{(n+p+1)!} \Big) \\ \end{align*} \]

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n \geq 1,\) \[ \sum_{i = 1}^n \dfrac{1}{\prod_{j = 0}^{p} (i + j)} = \dfrac{1}{p} \cdot \Big(\dfrac{1}{p!} - \dfrac{n!}{(n+p)!}\Big). \]

Exercice 4.6 (Renforcer l’hypothèse de récurrence) Démonter par récurrence les propriétés suivantes. Indication : on pourra renforcer l’hypothèse de récurrence en considérant non pas un seul rang, celui du prédécesseur, mais plusieurs rangs précédents.

1. Étant donné la suite \((u_n)\) définie par récurrence par \[ \begin{cases} u_0 = 1, \\ u_1 = 5, \\ u_{n+2} = u_{n+1} + 2 \cdot u_{n}, \\ \end{cases} \] pour tout entier naturel \(n,\) \[ u_n = (-1)^{n+1} + 2^{n+1}. \]
2. Pour tout entier naturel non nul \(n,\) \(n\) est égal à un produit de facteurs premiers (avec la convention naturelle que le produit de zéro facteur est égal à l’élément neutre de la multiplication, \(1,\) et que le produit d’un seul facteur est ce facteur).

from typing import NewType

Nat = NewType('Nat', int) # Type pour les entiers naturels (restriction de int aux positifs)

# constructeur de Nat en prenant la valeur absolue d'un int
def nat(val: int) -> Nat:
    if val < 0:
        return Nat(-val) # valeur absolue si négatif
        # alternative : raise ValueError("Un entier naturel doit être positif ou nul.")
    return Nat(val)

from decimal import Decimal # type pour calculer formellement, sans approximation

def testPropriete(prop, n) :
    for i in range(0, n) :
        if not prop(i) :
            return i, False
    return n, True

def u(n : Nat) -> Decimal :
   if(n == 0) :
      return Decimal(1)
   if(n == 1) :
      return Decimal(5)
   return u(n-1) + Decimal(2) * u(n-2)

Q = "?\n\t" # séparateur question / réponse
n = 20
print(f"forme explicite de u correcte {Q} Vérification pour les {n} premiers termes : {testPropriete(lambda j : u(j) == (Decimal(-1))**(j+1) + (Decimal(2))**(j+1), n)}")

forme explicite de u correcte ?
     Vérification pour les 20 premiers termes : (20, True)

Question 1 : Test de la formule explicite

Solution 1 - Relation de récurrence du second ordre

Considérons la propriété suivante[C’est une conjonction de deux propriétés, au rang \(n\) et au rang \(n-1.\) Pratiquement l’opérateur de conjonction est \(\wedge\) et se lit “et”.], pour \(n \in \Nat{}\) non nul : \[ u_n = (-1)^{n+1} + 2^{n+1} \wedge u_{n-1} = (-1)^{n} + 2^{n}. \]

Initialisation : \(n = 1.\) On a \(u_1 = 5\) et \((-1)^{1+1} + 2^{1+1} = 1 + 4 = 5\) d’une part, et \(u_0 = 1\) et \((-1)^{0+1} + 2^{0+1} = -1 + 2 = 1\) d’autre part, ce qui démontre la propriété en \(n = 1.\)

Hérédité : soit \(n \geq 1\) un entier naturel et supposons \[ u_n = (-1)^{n+1} + 2^{n+1} \wedge u_{n-1} = (-1)^{n} + 2^{n}. \] Montrons \[ u_{n+1} = (-1)^{n+2} + 2^{n+2} \wedge u_{n} = (-1)^{n+1} + 2^{n+1}. \] L’égalité pour \(u_n\) est immédiate puisqu’elle fait partie de l’hypothèse de récurrence. Il reste à montrer l’égalité pour \(u_{n+1}\). Or par définition de \(u_{n+1},\) égal à \(u_{n-1+2},\) et en appliquant l’hypothèse récurrence,

\[ \begin{align*} u_{n+1} &= u_{n} + 2 \cdot u_{n-1} \\ &= (-1)^{n+1} + 2^{n+1} + 2 \cdot ((-1)^{n} + 2^{n}) \\ &= -(-1)^{n+2} + 2 \cdot (-1)^{n+2} + 2 \cdot 2^{n+1} \\ &= (-1)^{n+2} + 2^{n+2}. \\ \end{align*} \]

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n \geq 1,\) \[ u_n = (-1)^{n+1} + 2^{n+1} \wedge u_{n-1} = (-1)^{n} + 2^{n}, \] ce qui implique pour tout \(n \in \Nat{},\) \[ u_n = (-1)^{n+1} + 2^{n+1}. \]

Solution 2 - Décomposition en facteurs premiers

Montrons par récurrence la propriété suivante, pour \(n\in\Nat{}\) non nul : tout entier naturel entre \(1\) et \(n\) est égal à un produit de facteurs premiers. On pourrait la formaliser ainsi, en notant \(\mathcal{P}\) l’ensemble des nombres premiers :
\[ \forall m \in \Nat{}, 1 \leq m \leq n \Rightarrow \exists k \in \Nat{}, \exists (p_1, \ldots, p_k) \in \mathcal{P}^k, m = \prod_{i = 1}^k p_i. \]

Initialisation : \(n = 1.\) \(1\) est un produit de zéro facteur premier.

Hérédité : soit \(n \geq 1\) un entier naturel et supposons que tout entier naturel entre \(1\) et \(n\) est égal à un produit de facteurs premiers. Montrons que tout entier naturel entre \(1\) et \(n+1\) est égal à un produit de facteurs premiers. Soit \(m\) un entier naturel entre \(1\) et \(n+1.\) Si \(m \leq n,\) il suffit d’appliquer l’hypothèse de récurrence. Sinon, supposons \(m = n+1.\) Si \(m\) est un nombre premier, \(m\) est égal à un produit d’un seul facteur, lui-même, qui est premier. Sinon, supposons que \(m\) n’est pas premier. Il se décompose sous la forme \(d_1 \cdot d_2\), avec \(1 < d_1 < m\) et \(1 < d_2 < m.\) Ainsi on peut appliquer l’hypothèse de récurrence à \(d_1\) et \(d_2\), qui sont deux entiers entre \(1\) et \(n\) : ils sont égaux chacun à un produit de facteurs premiers, si bien que leur produit \(d_1\cdot d_2\) est également un produit de facteurs premiers.

Conclusion : par application du principe de récurrence, on conclut que pour tout \(n \geq 1,\) tout entier naturel entre \(1\) et \(n\) est égal à un produit de facteurs premiers, ce qui implique que \(n\) est égal à un produit de facteurs premiers.

Exercice 4.7 (Trouver l’erreur) Les deux raisonnements par récurrence qui suivent sont faux. Trouver l’erreur et l’expliquer.

1. Démontrons par récurrence que tout entier naturel \(n,\) \(10^n + 1\) est un multiple de \(9.\) On a : \[ \begin{array}{rcl} 10^{n+1} + 1 & = & 10\cdot 10^{n} + 1 \\ & = & (9+1) \cdot 10^{n} + 1 \\ & = & 9\cdot 10^{n} + 10^n + 1. \\ \end{array} \] Donc si \(10^n + 1\) est un multiple de \(9,\) il en est de même de \(10^{n+1} + 1,\) ce qui démontre la propriété en appliquant le principe de récurrence.
2. Démontrons que tout entier naturel est égal à zéro. Considérons la propriété plus forte \[ \forall p \leq n, p = 0, \] et montrons la par récurrence.
   • Initialisation. Cette propriété est vraie pour \(n = 0.\)
   • Hérédité. Soit \(n\) un entier naturel, et supposons \(\forall p \leq n, p = 0.\) Montrons \(\forall p \leq n + 1, p = 0.\) Soit \(p \leq n +1.\) Envisageons deux cas. (i) Si \(p \leq n,\) par l’hypothèse de récurrence, \(p = 0.\) (ii) Si \(p = n + 1,\) par l’hypothèse de récurrence appliquée à \(n\) et \(1,\) on a \(n = 0\) et \(1 = 0,\) donc \(p = n + 1 = 0 + 0 = 0.\)
   • Conclusion. Par application du principe de récurrence, on conclut \(\forall n \in \Nat{}, \forall p \leq n, p = 0,\) d’où la propriété recherchée \(\forall n \in \Nat{}, n = 0.\)

Solution 1 - Multiplie de 9 ?

La démonstration prouve la propriété d’hérédité mais il manque l’initialisation. En \(n = 0,\) la propriété est fausse. La bonne propriété aurait été que \(10^n - 1\) est un multiple de \(9,\) pour \(n\) non nul.

Solution 2 - Nullité ?

La récurrence est complète au sens où l’initialisation et l’hérédité sont présentes. L’erreur est donc dans un des deux raisonnements. L’initialisation est correcte, il reste donc l’hérédité à examiner. Le premier cas est correct. Le second cas applique l’hypothèse de récurrence \(\forall p \leq n, p = 0\) à \(p = n\) et à \(p = 1.\) La première application est correcte mais la seconde, qui permet de déduire \(1 = 0,\) est possible si \(1 \leq n.\) Or \(n\) peut être nul. C’est l’erreur : il est impossible de réaliser la transition de \(0\) à \(1\) avec le raisonnement donné.

Exercice 4.8 (Suites récurrentes : démontrer génériquement la validité de la formule explicite) Soit \(f\) une fonction à deux paramètres¹² et \(c\) un réel. Soit \((u_n)\) une suite récurrente définie par \[ \begin{cases} u_0 = c, \\ u_{n+1} = f(u_{n}, n). \\ \end{cases} \]

1. Soit \(g\) une fonction telle que \(g(0) = c\) et pour tout entier naturel \(n,\) \[ g(n+1) = f(g(n), n). \] Montrer par récurrence que la suite \((u_n)\) a pour formule explicite \((g(n)).\) Rappel : la suite \((u_n)\) a pour formule explicite \((g(n))\) si pour tout entier naturel \(n, u_n = g(n).\)
2. Réciproquement, montrer que si la suite \((u_n)\) a pour formule explicite \((g(n)),\) alors \(g(0) = c\) et pour tout entier naturel \(n,\) \(g(n+1) = f(g(n), n).\)

Une récurrence générique

Cet exercice décrit exactement le travail à réaliser pour montrer par récurrence la validité d’une formule explicite pour une suite récurrente. L’initialisation revient à montrer que \(g(0) = c\) et l’hérédité revient à montrer que pour tout \(n,\) \(g(n+1) = f(g(n), n).\)

Exemple. \((u_n)\) est la suite définie par \(u_0 = 280\) et pour tout entier naturel \(n, u_{n+1}= (9/10) \cdot u_n + 42.\) Démontrer par récurrence que pour tout entier naturel \(n, u_n = -140 \cdot (9/10)^n + 420.\)

Ici la fonction \(f\) est définie par \(f(x, y) = (9/10) \cdot x + 42,\) et la fonction \(g\) par \(g(n) = -140 \cdot (9/10)^n + 420.\) Vérifions les deux conditions.

• \(g(0) = 280 :\) la première condition en \(0\) est vérifiée.
• Soit \(n\) un entier naturel. On a : \[ \begin{array}{rcl} f(g(n), n) & = & (9/10) \cdot (-140 \cdot (9/10)^n + 420) + 42 \\ & = & -140 \cdot (9/10)^{n+1} + (9/10) * 420 + 42 \\ & = & -140 \cdot (9/10)^{n+1} + (1 - 1/10) * 420 + 42 \\ & = & -140 \cdot (9/10)^{n+1} + 420 - 420/10 + 42 \\ & = & -140 \cdot (9/10)^{n+1} + 420 \\ & = & g(n+1). \end{array} \] La seconde condition est vérifiée.

Si vous développez la récurrence, vous rencontrerez ces deux conditions, pour l’initialisation et pour l’hérédité. Elles indiquent exactement les vérifications à réaliser.

Solution

Montrons par récurrence que pour tout naturel \(n, u_n = g(n)\).

• Initialisation : \(n = 0\). On \(u_0 = c\) et \(g(0) = c,\) si bien que la propriété est vérifiée.
• Hérédité. Soit \(n \in \Nat{}.\) Supposons \(u_n = g(n).\) Montrons \(u_{n+1} = g(n+1).\) Or \[ \begin{align*} u_{n+1} &= f(u_{n}, n) \quad \textrm{(définition)}\\ &= f(g(n), n) \quad \textrm{(hypothèse de récurrence)}\\ &= g(n+1) \quad \textrm{(définition)}.\\ \end{align*} \]

Réciproquement, supposons pour tout naturel \(n, u_n = g(n).\) En \(0,\) on obtient \(g(0) = c\) et par la relation de récurrence \(u_{n+1} = f(u_{n}, n),\) on obtient \(g(n+1) = f(g(n), n).\)

Exercice 4.9 (Théorème de Fermat-Wiles : vérification partielle) Le théorème de Fermat-Wiles affirme qu’il n’existe pas de nombres entiers strictement positifs \(x, y\) et \(z\) tels que : \[ x^n + y^n = z^n \] dès que \(n\) est un entier strictement supérieur à \(2.\)

On cherche à vérifier cette impossibilité dans un sous-domaine.

1. Soit \(x\) un réel strictement positif. Montrer par récurrence que pour tout entier naturel \(n \geq 2\), \[ (x + 1)^n > x^n + n \cdot x^{n-1}. \]

2. Soit \(p\) un entier naturel strictement supérieur à \(2\). Déduire de la première question que pour tout entier naturel \(n > p,\) \[ (p+2)^n > 2 \cdot (p+1)^n. \]

3. Soit \(p\) un entier naturel strictement supérieur à \(2\). Déduire de la première question que pour tout entier naturel \(n \geq p,\) \[ (p+2)^n > (p+1)^n + p^n. \]

Solution 1

Procédons par récurrence sur \(n\geq 2.\)

• Initialisation : \(n = 2.\) On a \((x + 1)^2 = x^2 + 2\cdot x + 1 > x^2 + 2 \cdot x^1,\) car \(1 > 0.\) L’inégalité stricte est donc vérifiée.
• Hérédité. Soit \(n\) un entier naturel tel que \(n \geq 2.\) Supposons \((x + 1)^n > x^n + n \cdot x^{n-1}.\) Montrons que \((x + 1)^{n+1} > x^{n+1} + (n+1) \cdot x^{n}.\) On a successivement : \[ \begin{align*} (x + 1)^{n+1} &= (x + 1) \cdot (x + 1)^{n}\\ &> (x + 1) \cdot (x^n + n \cdot x^{n-1}) \quad \textrm{(hypothèse de récurrence)}\\ &> x^{n+1} + (n+1) \cdot x^{n} + n * x^{n-1} \\ &> x^{n+1} + (n+1) \cdot x^{n} \quad (n * x^{n-1} > 0). \\ \end{align*} \]

Solution 2

Soit \(p\) un entier naturel strictement supérieur à \(2\). Appliquons l’inégalité montrée précédemment en \(x = p + 1.\) On obtient successivement, étant donné \(n > p :\) \[ \begin{align*} (p + 2)^n &> (p + 1)^n + n \cdot (p + 1)^{n-1} \\ &> (p + 1)^n + (p+1) \cdot (p+1)^{n-1} \quad (n \geq p +1)\\ &> 2 \cdot (p + 1)^n. \\ \end{align*} \]

Solution 3

Soit \(p\) un entier naturel strictement supérieur à \(2\). Appliquons l’inégalité montrée précédemment en \(x = p + 1.\) On obtient successivement, étant donné \(n \geq p :\) \[ \begin{align*} (p + 2)^n &> (p + 1)^n + n \cdot (p + 1)^{n-1} \\ &> (p + 1)^n + p \cdot p^{n-1} \quad (n \geq p, (p + 1)^{n-1} \geq p^{n-1})\\ &> (p + 1)^n + p^{n}. \\ \end{align*} \]

Vers un algorithme de vérification

La propriété démontrée permet de développer un algorithme qui vérifie qu’ effectivement, il n’existe pas de solution de l’équation \(x^n + y^n = z^n,\) étant donné un entier naturel non nul \(z.\) La recherche doit être exhaustive, mais comme elle serait alors infinie, on accepte l’élimination de certains cas lorsqu’on peut prouver élémentairement¹³ qu’aucune solution n’existe pour ces cas.

Commençons par restreindre les domaines de \(x\) et de \(y.\) Nécessairement \(x < z\) et \(y < z.\) Si \(x = y,\) on a \(2 \cdot x^n = z^n\), donc \(2\) divise \(z,\) et \(x^n = 2^{n-1} \cdot z_1^n,\) où \(z = 2 \cdot z_1,\) donc \(2\) divise \(x,\) et \(2 \cdot x_1^n = z_1^n,\) où \(x = 2 \cdot x_1,\) et ainsi de suite, en divisant par deux. Cette descente infinie en divisant par deux est impossible. Ainsi \(x \neq y ;\) supposons \(x > y.\) Comme la valeur maximale prise par la somme \(x^n + y^n\) est \((z - 1)^n + (z - 2)^n,\) limitons-nous à \(x := z - 1\) et \(y := z - 2.\)

Pour restreindre le domaine de l’exposant \(n\), utilisons la dernière majoration  : la somme \((z - 1)^n + (z - 2)^n\) est strictement inférieure à \(z^n\), lorsque \(z > 4\) et \(n \geq z - 2.\) Nous pouvons donc nous limiter aux cas complémentaires. Lorsque \(z > 4\), il reste à traiter les cas pour tout \(n < z - 2\) et pour les couples \((x, y)\) vérifiant \(z > x > y :\) ce doit être réalisé par l’algorithme. On peut en théorie se limiter à \(n = 4\) ou \(n\) impair et premier : pratiquement, il est plus simple de vérifier que l’équation ne tient pas. Lorsque \(z \leq 4,\) on a en appliquant la première inégalité à \(x = 3, 4^n > 3^n + n \cdot 3^{n-1}\), soit \(4^n > 2 \cdot 3^n\), puis à \(x = 2, 3^n > 2^n + n \cdot 2^{n-1},\) soit \(3^n > 2 \cdot 2^n,\) ce qui montre l’impossibilité d’une solution : ces cas peuvent être éliminés.

Continuons à restreindre le domaine de \(n\). Si \(x^n + y^n < z^n,\) on peut déduire \[ \begin{align*} x^{n + 1} + y^{n + 1} &< z \cdot x^n + z \cdot y^n \\ &< z \cdot(x^n + y^n) \\ &< z \cdot z^n \\ &< z^{n+1}. \\ \end{align*} \] Ainsi il est inutile de continuer dès que l’inégalité \(x^n + y^n < z^n\) est rencontrée.

Remarque : il est aussi possible de trouver une majoration pour \(n\) en résolvant l’inéquation \(2 \cdot (z-1)^n < z^n\), ce qui est possible en utilisant le logarithme : \(n > \dfrac{\logNat{}(2)}{\logNat{}(z/(z-1))}.\) Utilisant le logarithme, la preuve n’est pas élémentaire au sens que nous avons donné : certains résultats permettant la définition du logarithme sont admis en Terminale.

Voici donc le programme qui vérifie l’absence de solutions, après l’élimination des cas insolubles par une démonstration élémentaire. Il est désormais démontré que ce programme renvoie toujours True, mais la preuve n’est certainement pas élémentaire !

from decimal import Decimal # type pour calculer formellement, sans approximation

def testFermatWiles(z):
   if z <= 4 :
      return True
   # pour tout 5 <= zi <= z, boucle sur tous les couples (x, y) vérifiant z > x > y
   for zi in range(5, z + 1):  
      dz = Decimal(zi) 
      for x in range(4, zi):
         dx = Decimal(x)
         for y in range(3, x):
            dy = Decimal(y)
            px = dx**2
            py = dy**2
            pz = dz**2
            for n in range(3, zi - 2):
               px = dx * px
               py = dy * py
               pz = dz * pz 
               if (px + py == pz): 
                  return False, (x, y, zi, n)
               if(px + py < pz) :
                  break
   return True

print("Vérification du théorème de Fermat-Wiles :") 
print("     (False, (x, y, z, n)), avec x**n + y **n = z**n")
print("  ou True")
print("* z = 100 ? " + str(testFermatWiles(100)))

Vérification du théorème de Fermat-Wiles :
     (False, (x, y, z, n)), avec x**n + y **n = z**n
  ou True
* z = 100 ? True

4.5 Dérivation - Convexité

Exercice 4.10 (Approximation polynomiale d’un polynôme) Soit \(P\) une fonction polynomiale sur \(\Reel{}\) de degré trois : \[ P(x) := a_0 + a_1 \cdot x + a_2 \cdot x^2 + a_3 \cdot x^3, \] avec \(a_3 \neq 0.\)

1. Soit \(x_0\) un réel. Déterminer \(\alpha_0, \alpha_1, \alpha_2, \alpha_3\) de manière à vérifier pour tout \(x\) l’équation \[ P(x) = \alpha_0 + \alpha_1 \cdot (x - x_0) + \alpha_2 \cdot (x - x_0)^2 + \alpha_3 \cdot (x - x_0)^3. \] Indication : exprimer les coefficients \(\alpha_i\) en fonction de \(P(x_0), P'(x_0), P''(x_0), P'''(x_0)\), où \(P'\) (dite \(P\) prime) est la dérivée de \(P\), \(P''\) (dire \(P\) seconde) est la dérivée de \(P'\) et \(P'''\) (dite \(P\) tierce) est la dérivée de \(P''.\)
2. Déterminer l’équation en \(x_0\) de la tangente à la courbe représentant \(P.\) Soit \(D\) la fonction affine associée à la tangente.
3. Montrer que \(D\) est la meilleure approximation affine de \(P\). Indication : comparer la différence \(P - D\) avec toute autre différence \(P - A\), où \(A\) est une fonction affine vérifiant \(A(x_0) = P(x_0).\)
4. En analysant la différence \(P - D,\) étudier la convexité de \(P.\) Indication : étudier les cas \(P''(x_0) > 0\) et \(P''(x_0) < 0,\) puis \(P''(x_0) = 0,\) avec trois sous-cas \(P'''(x_0) > 0, P'''(x_0) < 0\) et \(P'''(x_0) = 0.\)

Exercice 4.11 (Inégalités de convexité)  

1. Soit \(\fctn{f}{\Reel{}}{\Reel{}}\) définie par \(f(x) = \valE{}^{x^2}\).
   1. Étudier la convexité de \(f\).
   2. Déterminer l’équation de la tangente à la courbe en \(1\).
   3. En déduire \(\forall x, f(x) \geq \valE{}\cdot (2\cdot x-1)\).
2. Suivant la même méthode, montrer \(\forall x \geq -1, (1+x)^{1/2}\leq (1/2)\cdot x+1\).

Solution

1. On utilise le résultat suivant du cours (Théorème en grande partie admis) :

   • \(f\) est convexe si et seulement si la dérivée seconde de \(f\) est positive.
   • \(f\) est convexe si et seulement si la courbe représentative de \(f\) est au-dessus de chacune de ses tangentes.
   1. Calculons \(f'\) puis \(f''\) en un réel \(x\).

   \[ \begin{array}{rcl} f\ x & = & \valE{}^{x^2},\\ f'\ x & = & 2 \cdot x \cdot \valE{}^{x^2},\\ f''\ x & = & 2 \cdot \valE{}^{x^2} + 4 \cdot x^2 \cdot \valE{}^{x^2},\\ & = & (2 + 4 \cdot x^2) \cdot \valE{}^{x^2}. \\ \end{array} \]

   On en déduit que \(f''\) est toujours positive : \(f\) est donc convexe.

   2. En \(1\), la dérivée vaut \(2 \cdot \valE{}\). La tangente passe par le point \((1, \valE{})\) et a pour équation : \(y = 2 \cdot \valE{} \cdot (x - 1) + \valE{}\), soit \(y = \valE{} \cdot (2 \cdot x-1)\).
   3. Comme \(f\) est convexe, chaque point \((x, (f\ x))\) de la courbe est au-dessus de la tangente en \(1\), soit \(\forall x, (f\ x) \geq \valE{} \cdot (2 \cdot x-1)\).

2. Soit \(\fctn{g}{[-1,+\infty[}{\Reel{}}\) définie par \(g(x) = (1+x)^{1/2}\).

   1. Calculons \(g'\) puis \(g''\) en un réel \(x\).

   \[ \begin{array}{rcl} g(x) & = & (1+x)^{1/2},\\ g'(x) & = & (1/2) \cdot (1+x)^{-1/2},\\ g''(x) & = & -(1/4) \cdot (1+x)^{-3/2}.\\ \end{array} \]

   On en déduit que \(g''\) est toujours négative : \(g\) est donc concave.

   2. On cherche \(x\) tel que la dérivée en \(x\) vaut le coefficient directeur de la droite \(y = (1/2) \cdot x+1\), soit \(1/2\). On trouve \(0\). La tangente passe par le point \((0 , 1)\) et a bien pour équation : \(y = (1/2) \cdot x + 1\).
   3. Comme \(g\) est concave, chaque point \((x, g(x))\) de la courbe est au-dessous de la tangente en \(1\), soit \(\forall x, g(x) \leq (1/2) \cdot x+1\).

Combes, et Bargues. 1977. Mathématiques, Terminales C et E, Exercices et problèmes avec solutions. Vuibert.

---

1. Une équation est linéaire si elle est de la forme réduite \(a \cdot x + b = 0,\) où \(x\) est l’inconnue et \(a\) et \(b\) sont des scalaires. C’est une équation du premier degré.

2. Elles sont dites commutatives car elles vérifient pour tous \(x\) et \(y, x + y = y + x\) et \(x * y = y * x.\)

3. Il y a \(5\) opérations, donc \(2^5\) commutations, soit \(32.\)

4. Ou toujours strictement négative, en raisonnant symétriquement.

5. C’est la droite d’équation \(y = x.\)

6. Dite décomposition en éléments simples. La théorie générale est étudiée dans le Supérieur. En Terminale, quelques cas simples sont rencontrés et peuvent être résolus facilement.

7. Il suffit d’analyser les différents cas, en partant de l’inégalité \(\beta \cdot x + b < \beta \cdot y + b,\) pour \(x < y.\) La comparaison entre \(1/(\beta \cdot x + b)\) et \(1/(\beta \cdot y + b)\) s’obtient en multipliant par les inverses, et suivant le signe du facteur, l’ordre est préservé ou inversé. On peut aussi raisonner d’une manière graphique, en utilisant la représentation de la fonction, une hyperbole.

8. On pourrait monter une majoration stricte.

9. On dit qu’un ensemble est stable par une opération si l’application de cette opération à des éléments de l’ensemble produit un élément de l’ensemble.

10. L’observation décisive est de relier \(111\) à son multiple \(999\) donc à \(1000 - 1\), le passage à \(10^6 - 1\) pouvant s’obtenir de différentes manières, celle indiquée mais aussi via l’identité remarquable \(10^6 - 1 = (10^3 - 1) \cdot (10^3 + 1).\)

11. On parle de télescopage (collision) des termes et de somme télescopique, par analogie avec un télescope, version longue-vue constituée de tubes qui se replient en s’emboîtant.

12. Une fonction qui à un couple de valeurs \((a, b)\) associe une valeur, égale à \(f(a, b).\)

13. Le sens d’élémentaire serait à préciser ! Mettons : ce que nous arrivons à prouver dans nos exercices de Terminale.